Pixel Recurrent Neural Networks

  • van den Oord, A., Kalchbrenner, N. & Kavukcuoglu, K., “Pixel Recurrent Neural Networks.” Proceedings of The 33rd International Conference on Machine Learning, in Proceedings of Machine Learning Research, 2016.

Summary

  • 이미지의 픽셀 생성시 Recurrent Neural Network(RNN)를 사용하며 다음 세 가지 Row LSTM, Diagonal Bi-LSTM, PixelCNN 모델을 제안한다.
  • $i$ 번째 픽셀을 (1 ~ $i-1$ )번째 픽셀을 이용하여 추론하는 Auto regressive propety를 갖고 tractable하다. 또한 log-liklihood측면에서 가장 우수한 성능을 보인다.
  • RNN의 특성으로 모든 이전 픽셀을 전부 사용할 경우 속도에 한계가 있어 receptive field를 삼각형으로 구성한다.
  • Diagonal Bi-LSTM은 $i-1$번째까지의 모든 픽셀을 사용하도록 구현되어 느리지만 성능이 우수하다.

Preliminaries

Autoregressive Property

Autoregressive를 갖는 PixelRNN은 이미지 생성시 $i$번째에 있는 픽셀 $x_i$의 확률 $p(x_i)$를 $i$보다 이전에 있는 픽셀을 이용해 구한다.

If the image $x$ is given as a one-dimensional sequence $𝑥_1,𝑥_2,…, x_{n^2}$, the joint distribution $𝑝(x)$ is written as:

\[\begin{align} p(x) = \Pi^{n^2}_{i=1}p(x_i|x_1, ..., x_{i-1}) \end{align}\]

pixel img

즉, Autoregressive를 따르는 모델은 새로운 픽셀의 확률분포를 주어진 다른(이전) 픽셀들의 확률분포로 구한다.

Long Short Term Memory

두번째로는 LSTM 모델에 대해 설명한다. Long Short Term Memory (LSTM)은 RNN계열 모델의 한 종류이다. RNN의 경우 시퀀스의 길이가 길어지면 gradient vanishing or explroding문제로 제대로 학습이 되지 않았다. 이는 순환신경망(반복적, 순차적으로 입력 값을 계산하는)의 특징이자 고질적인 문제이다. 이를 해결하기위해 LSTM은 cell state을 추가해 시퀀스의 길이(셀의 갯수)가 길어(많아)져도 gradient vanishing or explroding문제를 해결하고자 한다. 아래 중간 수식 (3)에서 나타내는 바가 이 cell state이다.

순환신경망모델이 자연어처리에 많이 사용되면서 자연어의 특성이 담긴 모델로 발전하기도 했는데, Bi-directional LSTM이 하나의 예시이다. 자연어처리는 어떤 한 단어를 선택할 때 앞에 놓인 단어 뿐만 아니라 뒤에 놓인 단어들도 참고해야하는 경우가 있다. 그러나 순환신경망은 한쪽 방향으로만 정보가 흐르기 때문에 이를 보완한 Bi-direcitonal LSTM이 등장했다. 주요한 핵심은 한쪽방향으로 흐르는 LSTM 레이어를 2개씩 사용해 하나는 순방향으로, 다른 하나는 역방향으로 입력을 계산하는 것이다. 아래 그림을 보면 보다 쉬운 이해가 가능할 것이라고 생각한다. 이후 두개의 셀에서 나온 출력들을 FC layer의 입력으로 사용해 최종출력한다. 이러한 구조는 본 포스팅에서 Diagonal LSTM 을 이해할때 큰 도움이 될 것이다. (특히 순방향 및 역방향 연산을 한다는 점을 유의.)

rowLSTM img

  • Note: $O$ refers output, $H$ refers hidden state with compuation arrow, $x$ refers input.

Comparison between Uni-directional (LEFT) and Bi-directional LSTM (RIGHT) (REF)

rowLSTM img

  • 본 예시에서 Uni-directional LSTM은 RowLSTM에 적용되고 Bi-directional LSTM은 Diagonal LSTM에 활용된다.

Models

이 섹션에서는 앞서 언급한 세개의 모델중 RNN을 활용하는 RowLSTM과 Diagonal Bi-LSTM을 활용한 모델을 설명한다. 이 섹션의 핵심은 autoregressive property를 지키면서 최대한 넓은 receptive field를 갖도록 각 RNN모델들의 적용방식이다.

Row LSTM

Row LSTM은 1D 컨볼루션으로 이미지를 행별로 처리하면서 receptive field는 아래 그림과 같이 삼각형 형태를 취한다.

rowLSTM img

일반적으로 삼각형 형태로 인해 모든 이전 픽셀을 활용하지 못한다고 생각할 수 있으나 이전 셀의 값을 입력으로 받아 연산하는 LSTM의 특성으로 이를 극복한다.

  • Long Short Term Memory (LSTM)
  • LSTM은 다음 input to state와 state to state을 계산한다. 각 셀 내에서 네트워크는 4개의 게이트를 통해 PixelRNN에서 입력-상태 구성요소는 먼저 행별로 이동하는 $k x 1$ 크기의 컨볼루션으로 전체 입력 맵에 대해 계산된다. 컨볼루션에서는 이전 픽셀만 포함하도록 마스킹되고(Masking 섹션에서 다룰예정) $4h, n, n$ 크기의 텐서를 생성합니다. 여기서 $h$는 출력 피쳐 맵의 크기이고 $n$은 이미지 치수이며 4는 LSTM 셀의 게이트 벡터 수입니다. 그런 다음 이전 상태에 컨볼루션을 적용하여 상태 대 상태 성분을 계산한다.
  • 수식은 아래와 같다:
\[\begin{align} [o_i, f_i, i_i, g_i] &= \sigma(K^{ss}\times h_{i-1}+K^{ss}\times x_i)\\ c_i &= f_i \cdot c_{i-1} + i_i \cdot g_i\\ h_i &= o_i \cdot tanh(c_i)\\ \end{align}\]

Note: $\times$ refers a convolution and $\cdot$ refers a dot production.

위와 같이 LSTM을 활용함에도 불구하고 아래 그림과 같이 어떤 셀 $x_i$ 와 같은 행에 있는 픽셀의 값을 참조하지 못하는 문제가 발생한다. 논문에서는 이를 위해 입력의 바로 왼쪽에 있는 셀(e.g., 초록색 셀)을 입력으로 제공한다.

rowLSTM img

코드를 보자면 다음과 같다. 먼저 셀의 구조를 보여주고 셀을 이용한 실제 모델 구현을 보인다. 해당 코드는 파이토치를 통해 작성되었다.

class RowLSTMCell(nn.Module):
    def __init__(self, hidden_dims, image_size, channel_in, *args, **kargs):
        super(RowLSTMCell, self).__init__(*args, **kargs)

        self._hidden_dims = hidden_dims
        self._image_size = image_size
        self._channel_in = channel_in
        self._num_units = self._hidden_dims * self._image_size
        self._output_size = self._num_units
        self._state_size = self._num_units * 2

        self.conv_i_s = MaskedConv1d(self._hidden_dims, 4 * self._hidden_dims, 3, mask='B', padding=_padding(image_size, image_size, 3))
        self.conv_s_s = nn.Conv1d(channel_in, 4 * self._hidden_dims, 3, padding=_padding(image_size, image_size, 3))
   
    def forward(self, inputs, states):
        c_prev, h_prev = states

        h_prev = h_prev.view(-1, self._hidden_dims,  self._image_size)
        inputs = inputs.view(-1, self._channel_in, self._image_size)

        s_s = self.conv_s_s(h_prev) #(batch, 4*hidden_dims, width)
        i_s = self.conv_i_s(inputs) #(batch, 4*hidden_dims, width)

        s_s = s_s.view(-1, 4 * self._num_units) #(batch, 4*hidden_dims*width)
        i_s = i_s.view(-1, 4 * self._num_units) #(batch, 4*hidden_dims*width)

        lstm = s_s + i_s
        lstm = torch.sigmoid(lstm)
        i, g, f, o = torch.split(lstm, (4 * self._num_units)//4, dim=1)

        c = f * c_prev + i * g
        h = o * torch.tanh(c)

        new_state = (c, h)
        return h, new_state

위에 코드 내용은 input-to-state연산과 state-to-state연산를 각기 구분하여 계산하는 것을 알수있다. 게다가 __init__함수를 보면 input-to-state연산에 Autoregressive property를 지키기 위해 Mask B를 활용한 것을 알 수 있다.

class RowLSTM(nn.Module):
    def __init__(self, hidden_dims, input_size, channel_in, *args, init='zero', **kargs):
        super(RowLSTM, self).__init__(*args, **kargs)
        assert init in {'zero', 'noise', 'variable', 'variable noise'}

        self.init = init
        self._hidden_dims = hidden_dims
       
        if self.init == 'zero':
            self.init_state = (torch.zeros(1, input_size * hidden_dims), torch.zeros(1, input_size * hidden_dims))
        elif self.init == 'noise':
            self.init_state = (torch.Tensor(1, input_size * hidden_dims), torch.Tensor(1, input_size * hidden_dims))
            nn.init.uniform(self.init_state[0])
            nn.init.uniform(self.init_state[1])  
        elif self.init == 'variable':
            hidden0 = torch.zeros(1,input_size * hidden_dims)
            ##if use_cuda:
            ##  hidden0 = hidden0.cuda()
            ##else:
            ##  hidden0 = hidden0
            self._hidden_init_state = torch.nn.Parameter(hidden0, requires_grad=True)
            self._cell_init_state = torch.nn.Parameter(hidden0, requires_grad=True)
            self.init_state = (self._hidden_init_state, self._cell_init_state)
        else:
            hidden0 = torch.Tensor(1, input_size * hidden_dims) # size
            nn.init.uniform(hidden0)
            self._hidden_init_state = torch.nn.Parameter(hidden0, requires_grad=True)
            self._cell_init_state = torch.nn.Parameter(hidden0, requires_grad=True)
            self.init_state = (self._hidden_init_state, self._cell_init_state)

        self.lstm_cell = RowLSTMCell(hidden_dims, input_size, channel_in)
    
    def forward(self, inputs, initial_state=None):
        n_batch, channel, n_seq, width = inputs.size()
        #print(n_seq)
        #inputs = inputs.view(n_batch, channel, n_seq, width)
        if initial_state is None:
            hidden_init, cell_init = self.init_state

        else:
            hidden_init, cell_init = initial_state

        states = (hidden_init.repeat(n_batch,1), cell_init.repeat(n_batch, 1))

        steps = [] # --> (batch, width * hidden_dims) --> (batch, 1, width*hidden_dims)
        for seq in range(n_seq):
            #print(inputs[:, :, seq, :].size())
            h, states = self.lstm_cell(inputs[:, :, seq, :], states)
            steps.append(h.unsqueeze(1))

        return torch.cat(steps, dim=1).view(-1, n_seq, width, self._hidden_dims).permute(0,3,1,2) # --> (batch, seq_length(a.k.a height), width * hidden_dims)
  • Note: RowLSTM 코드에서 __init__ 함수에서 파라미터 초기화를 선택할 수 있다. 초기화에 따라 성능이 다르니 시도해보는 것을 추천한다. 개인적인 구현 및 확인절차에서는 variable + gaussian noise 가 가장 좋은 성능을 보인다. 파이토치에서 순방향 연산을 나타내는 forward함수를 보면, RowLSTM방식은 기존의 LSTM을 이용한 연산과 거의 동일하다. LSTM셀에 순차적으로 넣고 이를 통해 최종 결과물을 내는 것을 확인할 수 있다. 특히 n_seq로 미리 모든 $x_i$에 대해 그 이전까지의 값을 시퀀스로 지정하고 loop을 통해 연산, 이후 붙혀 처리한다. 실제 구현단계에서 유의할 점은 reshape이 아닌 permute을 써야한다는 것이다. (reshape 및 permute의 차이)

Diagonal LSTM

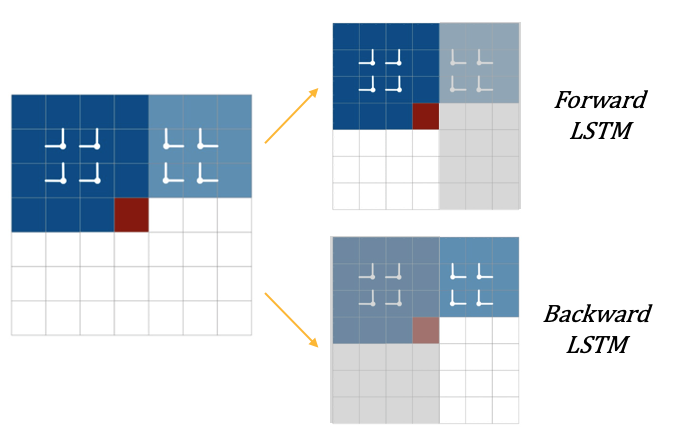
Diagonal LSTM은 삼각형태를 갖는 receptive field를 이상적인 형태 (i.e., 이전 모든 셀을 포함하는)로 만들기 위해 양방향 연산을 활용하는 Bidirectional LSTM을 사용한다.

diaLSTM img

  • 레이어의 두 방향 각각은 상단의 코너에서 시작하여 하단의 반대쪽 코너에 도달하는 대각선 방식으로 이미지를 사용한다.
  • 이로 인해 가장 넓은 receptive field를 갖게 되지만 두번의 연산과정으로 인해 제일 긴 계산시간을 갖는다. diaLSTM img
  • 구현방식에 있어서 Scewed Convolution을 제안한다.
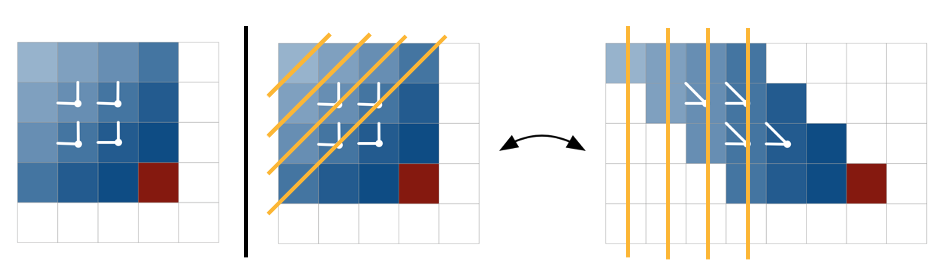
  • 이로인해 LSTM의 특성을 이용하면서도 효율적인 병렬 연산이 가능하다. 이해를 돕기 위한 그림은 아래와 같다. scew img

전체 연산 흐름은 다음과 같다. 먼저 input 맵을 이전 맵에 대해 각 행 $offset$이 1픽셀씩 있는 새 맵으로 왜곡하여 계산한다(scewed computation). 새 입력 맵의 최종 크기는 $n x *(2n-1)$ 이다. 두 방향 각각에 대해 input-state 구성요소( $1\times 1$ 컨볼루션)가 계산된다. state-state 구성 요소는 커널 크기( $2\times1$ )를 가진 열별 컨볼루션으로 계산된다. 출력 피쳐 맵은 $n \times n$ 차원으로 다시 압축된다.

정리하자면 diagnoal LSTM은 완전한 의존성 필드를 가지고 있다는 것이다. 또한 많은 수의 작은 계산( $2 \times 1$ 커널)을 사용함으로써 비선형적인 계산을 산출해 표현력이 향상된다고 생각한다.

Maskings and Residuals

Maskings

Autoregressive 모델을 구성하기 위해서는 데이터간 dependency 순서를 정해주는 것이 핵심적인데 이미지 픽셀의 dependency는 왼쪽위에서 오른쪽 아래 방향(본 포스팅의 첫 figure를 참조)으로 정의하고 색깔은 RGB 채널순서대로 종속성을 정의한다. masking img 위의 그림은 이전 셀만을 사용하도록 마스킹하는 것과 채널순서에 따라 마스킹하는 것을 함께 나타낸 그림이다. 위 그림에서 먼저 아래쪽그림들은 Mask A로 논문에선 기술되며 autoregressive property를 위해 셀 자신 이전의 셀만 입력되도록 마스킹 하는 것을 알 수 있다. 아래쪽에서 우측의 RGB채널들간 마스킹 역시 R채널은 이전 셀까지의 모든 정보를, G채널은 이전 셀 + R채널까지, B채널은 G채널까지 활용하도록 마스킹을 사용한다. 위 그림에 위쪽에 나타낸 그림들은 Mask B로 논문에서 기술하고 있으며 자기 셀 자신, 채널에선 동채널까지 입력으로 사용하고 있다.

정리하자면, Mask A로 어떤 셀 $x_i$ 이전까지의 셀로 한번 계산을 한 결과이기 때문에 Mask B계산에서 $x_i$의 위치를 포함시켜도 autoregressive property가 유지된다. 이해를 돕기 위해 첨부한 코드에서는 간단히 보이기 위해 흑백 이미지 사용을 목적으로 작성되었고 컬러 채널은 포함되어 있지 않다. 코드를 보면 A 타입은 필터의 중심도 가중치를 0 으로 셋팅하는 것이고 B 타입은 필터의 중심의 값을 이용한다. A 타입은 입력 이미지에 대해 첫번째 계산때만 사용하고 그 이후의 콘볼루션에서는 모두 B 타입을 사용한다. 흑백이 아니고 컬러 이미지일 경우 RGB 컬러가 각각 계산되어야 하기때문에 픽셀 레벨이 아닌 채널 레벨로 콘볼루션이 된다. 위에서 설명했듯, 컬러일 경우 A 타입은 현재 컬러 채널은 사용하지 않고 B 타입은 자기 컬러 채널도 콘볼루션에 이용하는 식이다.

def conv2d(input, num_output, kernel_shape, mask_type, scope="conv2d"):

    with tf.variable_scope(scope):

        kernel_h, kernel_w = kernel_shape
        center_h = kernel_h // 2
        center_w = kernel_w // 2

        channel_len = input.get_shape()[-1]
        mask = np.ones((kernel_h, kernel_w, channel_len, num_output), dtype=np.float32)
        mask[center_h, center_w+1:, :, :] = 0.
        mask[center_h+1:, :, :, :] = 0.
        if mask_type == 'A':
            mask[center_h, center_w, :, :] = 0.

        weight = tf.get_variable("weight", [kernel_h, kernel_w, channel_len, num_output], tf.float32, tf.contrib.layers.xavier_initializer())
        weight *= tf.constant(mask, dtype=tf.float32)

        value = tf.nn.conv2d(input, weight, [1, 1, 1, 1], padding='SAME', name='value')
        bias = tf.get_variable("bias", [num_output], tf.float32, tf.zeros_initializer)
        output = tf.nn.bias_add(value, bias, name='output')

        return output

이 코드의 핵심은 mask 배열로 가중치와 같은 사이즈로 만든 다음, 가운데 왼쪽과 위쪽만 1 값을 남기는 부분이다. 그런 다음 이 배열을 가중치 weight 와 곱하면 가중치 배열의 중앙 왼쪽과 위쪽만 남게 됩니다. MASK Type A 일 경우, 정중앙의 마스크 값도 0 으로 둔다. 그리고 ‘SAME’ 패딩을 사용해서 입력과 출력 이미지의 크기를 동일하게 맞줘 동일한 크기의 이미지를 출력하기 위함이다.

Residuals

Pixel RNN은 최대 12단 LSTM을 사용하는데 이때의 그라데이션 소실 또는 폭발 문제를 방지하기 위해 residual connection을 활용한다.

  • input-state 연산에서 게이트당 $h$ 크기의 피쳐를 생성함으로써 피쳐의 수를 줄이며, 이는 $1\times1$ Conv를 통해 업샘플링된다.
  • Skip connection 또한 residual connections의 일부로도 활용되며 각 계층에서 skip connection을 사용하여 결과를 출력한다.
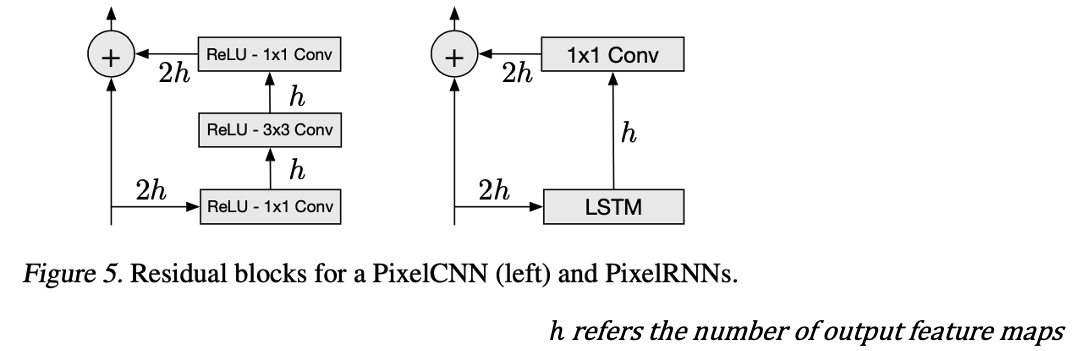
  • Pixel CNN과 RNN간 다른 형태의 residual connection이 사용되면 그림은 아래와 같다. masking img

Performance

모델 측면에서의 비교

먼저 논문에 소개된 모델들을 비교하자면 다음과 같다.

  • masking img

또한 앞서 설명한 residual connection 및 layer의 수에 따른 결과 비교는 다음과 같다.

  • masking img
  • masking img

보인바와 같이 residual과 skip connection을 활용해 깊은 신경망을 쌓았을때 NLL결과가 가장 낮은 것을 확인할 수 있다.

실험 결과에 따른 이미지 비교

CIFAR-10과 ImageNet 데이터셋을 통해 보인 정성적 결과들은 다음과 같다. masking img 아래 결과는 이미지 생성 테스트를 한 결과이며 가장 우측에 있는 그림이 원본이다. 중간에 있는 그림들이 모델이 출력한 결과이다. masking img

Conclusion

이 포스팅을 통해 PixelRNN에 대한 이해도가 높아졌길 바라며 정리한 이 논문의 핵심은 다음과 같다. pixelrnn은 새로운 픽셀의 확률 분포를 주어진 다른 픽셀들의 확률 분포로 가정한다. 그리고 각 픽셀의 색(RGB)의 값들도 순서대로 conditional하게 주어진다고 가정한다. 그리고 각 픽셀의 값의 분포를 continuous가 아닌 discrete로 가정하고 softmax를 통하여 추정하였다. 이렇게 다른 픽셀들로 부터 sequential하게 정보를 받는 방법으로 세가지 모델을 제안하였다. Pixel Recurrent Neural Networks라는 논문에서 PixelRNN, PixelCNN이 갖고 있는 구조가 모두 소개된다.

  • NLL을 기준으로 하였을때 기존보다 나은 image generation이 이루어졌다. PixelRNN은 이산 분포를 사용하여 이미지를 모델링하며, 이를 통해 모델이 더 나은 NLL 결과를 갖도록 이끈다.
  • 모델에서 LSTM을 사용해 autoregressive모델을 구현하는 두 가지 다른 방법이 제안되며, 이는 주어진 task의 조건(성능 및 시간)에 따라 선택을 가능하게 한다.