NICE

제가 리뷰하게 된 논문은 “NICE: NON-LINEAR INDEPENDENT COMPONENTSESTIMATION” 입니다. 해당 논문의 목적은 normalizing flow를 이용해 true likelihood와 가장 유사한 likelihood( $p(x|h)$ )를 학습하는 것입니다. 우선 리뷰를 시작하기전에 리뷰에 필요한 몇가지 background에 대해 설명드리겠습니다.

0. Background

0-1. Transformation of random variables

우선 가장 첫번째로 알아야 하는 개념은 Transformation of random variables입니다. 해당 개념은 문자 그대로 확률 변수(random variables)를 다른 확률 변수로 변환(transformation)하는 기법입니다. 만약 연속 확률변수 $X, Y$가 존재하고 $Y = g(X)$가 단조 증가, 단조 감수 함수일 경우에 아래와 같은 식을 통해 $Y$의 pdf를 구할 수 있습니다.(편의상, 또한 이에 대한 많은 자료가 있기에 증명은 생략토록 하겠습니다.)

위 식에서 $J = { {\partial{y} }\over{\partial{x} } }$를 jacobian matrix, $\lvert J\rvert$를 determinant라 합니다. 본 논문에서 determinant의 역할에 대해서 계속해 언급되는데 간단한 예를 통해 알아볼 수 있도록 하겠습니다.

아래와 같은 확률 변수 $X$와 pdf $p_{X}$를 가정하겠습니다.

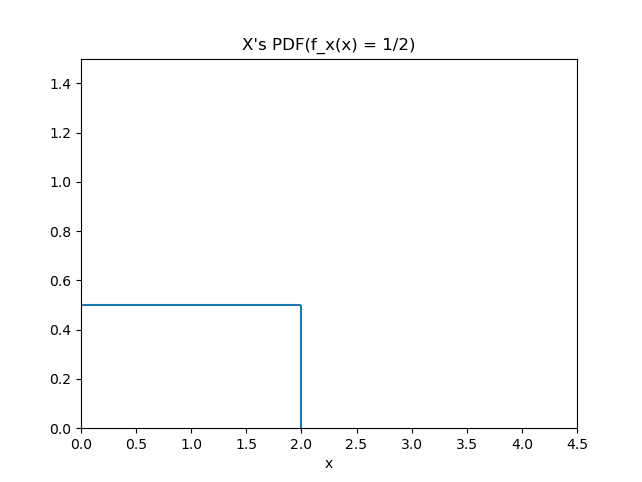
이후 $Y = g(X) = { {X}\over{2} }, Z = g’(X) = 2X$인 확률 변수 $Y, Z$를 가정하고 다음과 같이 $p_{Y}(y), p_{Z}(z)$를 구해보도록 하겠습니다.

$Y$의 경우 ${\lvert J\rvert} = { {1}\over{2} }$이고 그림을 통해 분포가 좁아진 것을 확인할 수 있습니다. $Z$의 경우 $\lvert J\rvert = 2$이고 분포가 넓어진 것을 확인할 수 있습니다. 즉 determinant $\lvert J\rvert$는 분포의 퍼진 정도에 영향을 주며 커질수록 분포가 넓어지고(expansion) 작아질수록 분포가 좁아지는(contraction) 현상을 관찰할 수 있습니다. 비록 위 예는 아주 간단한 uniform distribution을 통해 현상을 관찰하였지만 좀 더 복잡한 분포에서도 이러한 성질은 유지됩니다. Expansion과 contraction은 본 논문에서도 반복해서 사용되는 용어이기 때문에 위 예와 함께 determinant의 역할을 기억해주시면 앞으로 리뷰를 이해하는데 큰 도움이 될 수 있습니다.

0-2. Normalizing Flow

0-1에서도 관찰 할 수 있듯이 특정 확률 변수와 그 분포는 어떠한 변환(함수)에 의해 다른 분포를 가질 수 있습니다. 위에서 설명드린 예시들은 uniform distribution을 uniform distribution으로 변환 시키는 과정을 보여드렸지만 조금 더 복잡한 형태의 변환을 보여드리고 normalizing flow에 대해 설명드리겠습니다. 일단은 전과 같이 uniform distribution을 가지는 확률 변수 $X$를 가정하겠습니다.(위와 같은 확률 변수 $X$입니다.)

이때 $Y=g(X)= X^{2}+X$의 학률 분포는 다음과 같습니다.

이때 또 한번 $Z=g’(Y)=log(Y+1)$을 만족하는 확률 변수 $Z$를 정의하면 그 확률 분포는 다음과 같습니다.(편의상 계산 과정은 생략하였습니다.)

식만 보아도 형태가 비교적 복잡한 것을 확인할 수 있습니다. 이 분포를 그림으로 표현하면 아래와 같습니다.

$X, Y, Z$의 각각 분포를 관찰하면 uniform 형태에서 비선형 형태, 단순 증가, 감소함수가 아닌 형태로 분포가 조금씩 변형되는 것을 확인할 수 있습니다. 즉, 비교적 간단한 형태의 분포도 transformation of random variables를 사용하여 형태를 조금씩 변형해줄 수록 좀 더 복잡한 형태의 분포를 가질 수 있습니다. 만약 충분히 많은 횟수, 충분히 복잡한 함수를 사용하여 변형한다면 상당히 복잡한 형태의 분포도 표현할 수 있을 것으로 생각됩니다.

‘Normalizing flow’란 위와 같은 성질을 이용하는 기법이라고 할 수 있습니다. 많은 종류의 생성모델은 loglikelihood( $p(X)$ )를 최대화하려는 목적을 가지고 있습니다. 이러한 관점에서 볼 때 $p(X)$가 주어진 데이터를 표현할 수 있을 만큼 충분히 복잡한 형태이면 좋을 것 입니다. 그러나 기존 ‘VAE’와 같은 방법론들은 $p(X)$를 복잡하게 표현하기에 한계가 있기에 normalizing flow에서는 아래와 같은 과정을 통해 이러한 한계를 극복하고자 합니다.

위 식은 $z_{i}$의 분포가 $z_{i-1}$의 분포로부터 $f_{i}$의 transformation을 통해 생성되는 연속적인 과정을 나타내고 있습니다. 이를 그림으로 나타내면 아래와 같습니다.

Transformation이 진행될 수록 좀 더 복잡한 형태의 분포가 생성되는 것을 관찰할 수 있습니다. 이제는 이를 좀 더 일반화한 식으로 표현해 보도록 하겠습니다.

이를 계산하기 좀 더 쉽도록 log형태로 바꾸고 $z_{K} = x$임을 활용하면 다음과 같이 나타낼 수 있습니다.

즉 normalizing flow란, 위와같은 식을 통하여 비교적 간단한 형태의 분포( $p_{0}(z_{0})$ )로 부터 복잡한 형태의 분포( $p(x)$ )를 계산해내는 기법이며 이를통해 기존의 다른 생성 모델에서는 얻지 못했던 복잡한 형태의 $p_{x}$를 얻을 수 있다. 다만 이에 대한 몇가지 제한이 있는데 이는 다음과 같습니다.

1. 역함수( $f^{-1}$ )가 계산하기 쉬운 형태여야 한다.
2. Determinant를 계산할 수 있어야 한다. $\leftarrow$ Jacobian이 정사각 행렬 형태로 나오도록 x, z의 차원수가 같아하고 determinant를 계산하기 용이한 형태여야 한다.

따라서 normalizing flow를 활용하는 많은 생성 모델들은 위 제한을 지키되 복잡한 $p(x)$를 보장하도록 $f$의 형태를 복잡화하는데 주안점을 두고 있습니다.

1. Objective function of NICE

이제 본격적으로 본 논문의 모델 NICE에 대해 알아보도록 하겠습니다. NICE는 위에서 설명한 normalizing flow를 사용하는 flow 계열 모델입니다. 아주 간단한 prior( $p_{H}(h)$ )로 부터 복잡한 likehood( $p_{X}(x)$ )를 최대화할 수 있도록 학습을 진행합니다. 이때 deteminant를 계산할 수 있도록 input vector( $x$ )와 hidden vector( $h$ )의 차원은 같게 하도록 하며 $p_{h}(h)$ 는 각 성분이 독립이고 다음과 같이 factorize하게 분해되는 형태로 가정합니다.

이러한 prior 확률 변수 $h$와 input 확률 변수 $x$가 $h=f(x)$의 관계를 만족 시키면 다음 식과 같이 transformation을 적용할 수 있습니다.

이후 다음과 같이 연산하기 쉽도록 log 형태로 바꾸어 줍니다. 아래의 $f(x)$ 가 $f_{d}(x)$ 로 분해되는 과정은 $H$의 성분 별로 다른 transformation을 적용하여 좀 더 복잡한 $H$를 만들기 위함입니다. 이는 뒤에서 좀 더 다룰 수 있도록 하겠습니다.

위와 같은 형태는 determistic한 식으로써 연산간에 sampling이 전혀 필요가 없습니다. 따라서 일반적인 opimization 방법들(gradient ascent)을 사용해서 쉽게 maximization할 수 있습니다. 이제 maximize해야 하는 objective function을 결정했으니 역함수와 determinant를 쉽게 구할 수 있는 $f(x)$를 결정할 차례입니다.

2. Structure of NICE

2-1. General Coupling Layer

우선은 determinant를 쉽게 구할 수 있는 $f_(x)$를 만드는데 집중해보도록 하겠습니다. Determinant를 쉽게 구할 수 있는 행렬은 대표적으로 삼각행렬이 있습니다. 삼각행렬의 determinant 값은 다음과 같이 대각 성분의 곱을 통해 구할 수 있습니다.

따라서 본 논문에서도 jacobian을 삼각행렬로 만들기 위한 $f_(x)$를 구성합니다. 이를 위해 input $x$와 output $y$를 분해해서 연산을 진행하며 이러한 구조를 coupling layer라고 합니다. 분해 방식은 다음과 같습니다. $x$가 $D$차원 vector일 때 $\lvert I_{1}\rvert=d$와 $\lvert I_{2} \rvert =D-d$크기를 갖는 $x_{I_{1} }, x_{I_{2} }$으로 분해합니다. 그리고 output $y_{I_{1} }, y_{I_{2} }$를 아래와 같이 구성합니다.

전에 언급했듯이 determinant를 계산하기 위해서는 jacobian matrix가 정방 형태여야 합니다. 따라서 $y$도 $D$ 차원이 될 수 있도록 $g$ 함수는 $\mathbb{R}^{D-d} \times m(\mathbb{R}^{d}) \rightarrow \mathbb{R}^{D-d}$ 형태로 구성되어야 합니다. 또한 $y$의 연산 과정에 비선형 활성화 함수를 포함한 MLP(Mulit Layer Perceptron)( $m(x)$ )를 포함시켜 충분히 복잡한 output을 생성할 수 있도록했습니다. Coupling layer의 이러한 형태로 인해 아래와 같은 삼각행렬 형태의 jacobian을 얻을 수 있습니다.

결론적으로 해당 jacobian의 determinant는 대각 성분의 곱으로 아래와 같이 되며 $y_{2}$에 복잡한 형태의 $m(x_{I_{1} })$가 포함되어 있지만 삼각행렬의 determinant 정의에 따라 ${ {\partial{y_{I_{2} } } }\over{\partial{x_{I_{1} } } } }$는 전혀 계산할 필요가 없어집니다.

이러한 deteminant를 갖도록 설계한 layer를 General Coupling Layer라고 합니다. 이제는 이러한 general한 형태의 coupling layer로 부터 $\det{ { {\partial{y_{I_{2} } } }\over{\partial{x_{I_{2} } } } } }$ 와 그 역함수를 쉽게 계산할 수 있는 $g$를 선택해야 합니다.

2-2. Additive Coupling Layer

앞서 정의한 general coupling layer는 jacobian matrix를 비교적 간단한 형태로 함으로써 determinant의 손쉬운 계산을 가능하게 해줬습니다. 하지만 여전히 $\det{ { {\partial{y_{I_{2} } } }\over{\partial{x_{I_{2} } } } } }$ 와 $g^{-1}$을 계산할 수 있는 $g$를 선택해야하는 과제가 남아있습니다. 이러한 과제를 해결하기 위한 가장 간단한 방법은 $g$를 다음과 같이 간단한 합연산만을 포함한 함수로 선택하는 것입니다.

이러한 $g$를 선택하면 다음과 같이 아주 간단하게 output $y$로 부터 input $x$를 계산할 수 있습니다.(역함수를 구할 수 있습니다.)

또한 $\det{ { {\partial{y_{I_{2} } } }\over{\partial{x_{I_{2} } } } } } = 1$인것도 매우 쉽게 확인할 수 있습니다. Addictive coupling layer란 이처럼 $g$를 합연산을 통해 구현하여 general coupling layer에서는 여전히 남아있는 문제들을 해결한 coupling layer입니다. 이에대한 coumputational graph는 아래와 같습니다.

그림을 보면 위에 설명한 구조와 똑같아서 이해하기 쉬우시겠지만 표기들이 달라 이에대해 간단히 언급하자면 $x_{key} = x_{I_{1} }, y_{key} = y_{I_{1} }, x_{plain} = x_{I_{2} }, y_{cipher} = y_{I_{2} }$ 입니다. 사실 이러한 용어 선택에 대한 질문을 받았었는데 제가 저자가 아니기 때문에 정확히는 잘 모르겠습니다. 그치만 한번 유추해 보자면 $key = I_{1}$은 일단 $x_{key}$와 $y_{key}$에 공통으로 사용함으로써 input이 바로 output이 되어 변하지 않는다는 의미를 내포하는 것 같습니다. $plain$은 ‘솔직한’, ‘있는 그대로의’, ‘분명한’과 같은 뜻을 갖고 있는데 이는 아마 $x_{I_{2} }$가 $y_{I_{2} }$로 될 때 그대로 더해지니까 선택한 단어가 아닌가 합니다. $cipher$는 ‘암호’라는 뜻을 갖고 있는데 이는 $x_{I_{1} }$이 비선형 함수 mlp를 지나 $x_{I_{2} }$와 더해져 $y_{I_{2} }$가 만들어 지기 때문에 output으로써 해석하거나 이해할 순 없지만 데이터의 여러 특징들을 반영한 벡터가 되기를 원하기 때문이 아닐까 합니다. 다만 이부분은 순전히 개인적인 생각이니 다른 주장이 있으면 말씀해주시면 감사드리겠습니다 :)

자, 여러분 벌써 여기까지 왔습니다. 이러한 additive coupling layer로도 충분히 생성 모델을 만들어 낼 수 있을 것 같습니다. 그러나 너무 아쉽게도 아직 2가지 한계가 있습니다. 첫번째는 바로 coupling layer에서는 $x_{I_{1} }$이 그대로 $y_{I_{1} }$이 되어버린 다는 것 입니다. 저희가 애초에 normalizing flow 기법을 쓰는 이유가 충분히 복잡한 $p(x)$를 만들기 위함이잖아요? 근데 input의 일부분이 그대로 output이 되어버린다니… 이런식이면 input과 output이 선형성으로만 유지되는 부분이 생기고 복잡한 $p(x)$를 생성해내지 못하게 됩니다!

또한 determinant를 너무 간단히 만들려다 보니까 $\det{ { {\partial{y_{I_{2} } } }\over{\partial{x_{I_{2} } } } } }$가 그냥 1이 되어버렸습니다. 앞서 설명드린 것 처럼 determinant의 역할은 expansion과 contraction인데 이는 transformation 과정간 아주 중요한 역할을 담당하고 있습니다. 따라서 determinant가 1인 것도 additive coupling layer의 한계라 볼 수 있습니다. 따라서 다음 과정은 이러한 한계점들을 극복하기 위한 방안을 제시합니다.

2-3. Combining Coupling Layers

$x_{I_{1} }$이 그대로 $y_{I_{1} }$이 되는 문제는 비교적 간단히 해결할 수 있습니다. Coupling layer를 여러 층으로 쌓고 한개의 coupling layer마다 $x_{I_{1} }$과 $x_{I_{2} }$를 교체하면 됩니다. 이를 그림으로 표현한 것은 다음과 같습니다.

그림처럼 coupling layer마다 $I_{1}, I_{2}$를 구성하는 방법을 뒤바꿔주면 결국엔 input이 완전히 바뀔 수 있을 것 입니다.( $x$ 와 $z$의 변화를 통해 쉽게 확인할 수 있습니다.) 또한 본 구현에서는 그림과 같이 $I_{1}, I_{2}$를 구성할 때도 약갼의 복잡성을 추가하기 위해 데이터의 홀수별, 짝수별로 구성하였습니다. 여기서 어떤분은 ‘근데 왜 $I_{1}, I_{2}$을 꼭 $D/2$ 차원으로 구성할까?’라는 의문이 드실 수 있을 것 같습니다. 이에 대한 이유는 다음과 같습니다. 물론 기본적으로는 꼭 $I_{1}, I_{2}$를 꼭 $D/2$ 차원으로 구성할 필요는 없습니다. 다만 구현 과정에 있어서 $y_{I_{2} } = x_{I_{2} } + m(x_{I_{1} })$이기 때문에 $m(x_{I_{1} })$과 $y_{I_{2} }$의 차원은 같아야 합니다. 근데 만약 input을 분해할 때 차원을 똑같이 구성해 주지 않는다면 다음 layer에서는 $x_{I_{1} }$과 $x_{I_{2} }$가 뒤바뀌어야 함으로 이를 위한 $m(x)$를 따로 설계해야 겠죠… 따라서 이러한 불필요한 설계를 줄이기 위해 $I_{1}, I_{2}$을 간단히 $D/2$ 차원으로 구성한 것 같습니다. 만약 input, output의 차원을 같도록 설정할 수 있다면 input을 굳이 $D/2$ 차원으로는 분해할 필요가 없다고 생각합니다.

2-4. Allowing rescaling

이쯤에서 다시한번 처음으로 돌아가 저희의 objective function을 확인해보겠습니다.

이제는 coupling layer을 통해 드디어 위 objective function을 최적화시킬 수 있습니다! 그치만 한가지 안타까운 점은 $\det{ { {\partial{y_{I_{2} } } }\over{\partial{x_{I_{2} } } } } }$가 1이되어 $log(\lvert \det{ { {\partial{f(x)} }\over{\partial{x} } } }\rvert)$ 항이 0이 되어버린다는 것 입니다. ‘0-1’ 항목에서 보았듯이 determinant는 분포의 expansion, contraction에 영향을 줍니다. 따라서 determinant가 1이 되어 역할을 못한다는 것은 분포의 transformation 과정에 있어서 복잡성을 떨어뜨려 복잡한 true loglikelihood, $p(x)$를 구하는데는 악영향을 끼칠 것 입니다.

이를 해결하기 위해 가장 마지막 coupling layer의 output에 digonal scaling matrix를 곱해주어 determinant의 역할을 할 수 있도록 도와줍니다. 즉, 각 $i$ 차원의 성분은 $(x_{i})_{i\le D} \rightarrow (S_{ii}x_{i})_{i\le D}$와 같이 변환됩니다. 이때 objective function은 다음과 같이 수정되며 구현상 $\lvert S_{ii} \rvert$를 사용하는 것보다 $e^{s_{ii} }$를 대신해서 사용하는 것이 더욱 간단하기 때문에 $e^{s_{ii} }$를 사용하였습니다.

그렇다면 이 $S$는 어떤 역할을 할 수 있을까요? 여기서부터는 필자의 자의적인 해석이 어느정도 포함되므로 틀린 사실이 있으면 바로 정정해주시길 바라겠습니다. 저희는 ‘0-1’ 항목에서 아래와 같은 식에서 determinant $\lvert J \rvert$가 커질수록 transformation시 분포가 expansion하고 작을수록 contraction된다는 사실을 관찰하였습니다.

NICE의 변경된 objective function을 다음과 같습니다.

여기서 $f_{i}(x)$를 편의상 $h_{i}^{-1}(x)$로 교체해서 적겠습니다.(유사성을 보여주기 위한 편의상의 조치입니다. 어차피 $f$는 역함수가 존재한다고 가정하니 $f=h^{-1}$라고 생각해주시면 될 것 같습니다.)

NICE의 objective function의 형태를 조금 바꾸니 원래의 transformation of variables랑 형태가 같다는 것을 확인할 수 있습니다. 즉 $\lvert S_{ii} \rvert$는 $\lvert { {1}\over{J} }\rvert$의 역할을 수행하도록 만들어진 것 입니다. 앞선 예시에서 $\lvert J \rvert$가 커질수록 분포가 넓어지고 작아질수록 분포가 좁아지는 역할을 수행하는 것을 확인하였습니다. $\lvert S_{ii} \rvert$는 그 역수이므로 커질수록 분포가 좁아지고(contraction) 작아질수록 분포가 넓어지는(expansion) 역할을 수행하게 됩니다. 즉, $\lvert S_{ii} \rvert$ 커질수록 contraction이 심하게 일어나서 해당 차원의 분포는 좁아지게 되어 $p_{X}(x)$는 해당 차원을 의미없는 차원으로 여기게 됩니다. 반대로 $\lvert S_{ii} \rvert$가 작아질수록 expansion이 심하게 일어나서 해당 차원의 분포는 넓어지게 되며 $p_{X}(x)$는 해당 차원의 많은 정보를 사용하므로 상당히 유의미한 차원으로 여기게 됩니다. 이렇듯 차원의 expansion과 contraction을 통해 $p_{X}(x)$를 좀더 풍부하고 복잡하게 만들도록 하는 것이 $S$의 역할입니다.

2-5. Prior Distribution

해당 부분은 NICE의 structure에 대한 부분이라기 보다는 그냥 prior($H$)의 분포를 정하는 파트입니다. 사실 prior는 transformation을 거치며 복잡한 데이터의 분포로 변형될 것이기 때문에 크게 중요한 부분은 아닌 것 같습니다. 대신 그래도 어느정도는 복잡한 것이 좋을 것 같습니다. 따라서 본 논문에서는 앞서 언급한 것처럼 prior를 gausian 또는 logistic distribution으로 결정합니다. 딱히 중요하다고 생각되지 않는 파트기에 gausian distribution과 logistic distribution의 log 형식을 식으로 보여드리고 넘어가도록 하겠습니다.

• Gausian distribution

• Logistic distribution

2-6. Code Implementation

이번 section에서는 NICE의 코드를 간단히 보여드리도록 하겠습니다. Paul Tang님의 github에 있는 코드를 설명을 위해 조금 변형하였습니다.

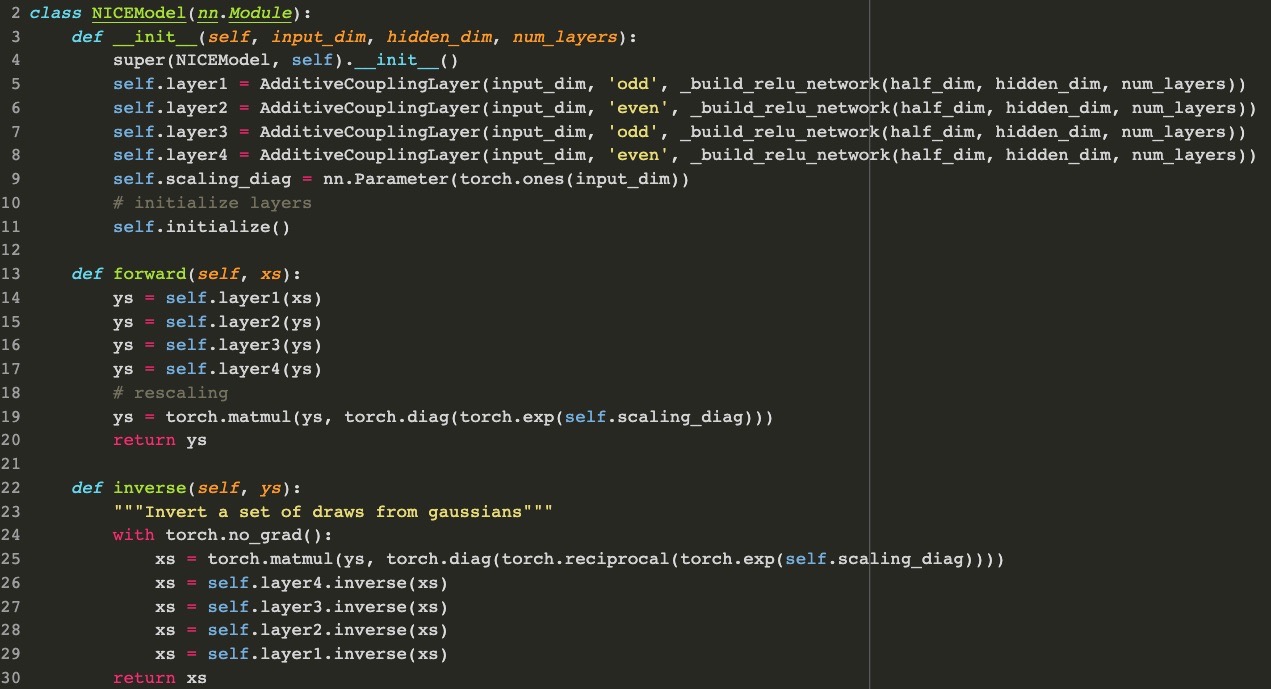
코드 1에서 볼 수 있듯이 Nice모델은 여러 개의 Additive coupling layer로 이루어져 있으며, 모든 layer 통과 후 하나의 rescaling layer가 존재함을 볼 수 있다. Inverse의 경우 forward의 정확한 역순이다.

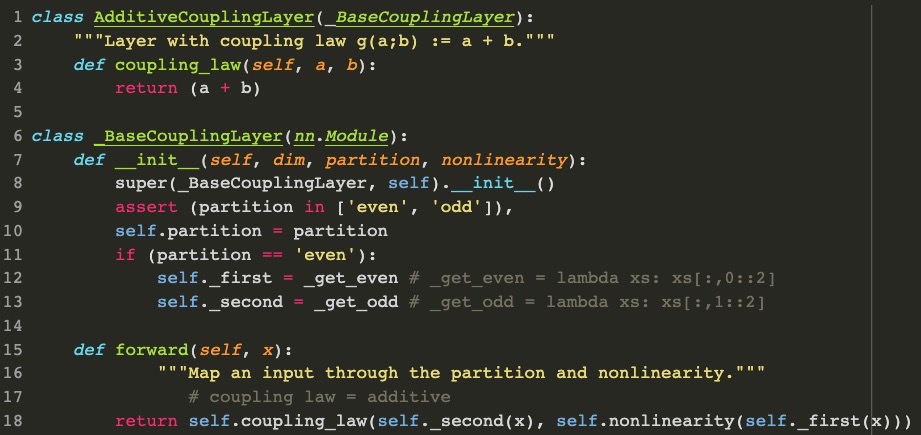
코드 2는 Additive coupling layer의 코드이다. Coupling law는 a+b로 되어 있다. Parition law같은 경우 index를 0부터 시작할지 1부터 시작할지가 다를 뿐 전체를 하나씩 건너서 총 두개의 part로 partition해주는 것을 볼 수 있다. Forward의 경우, 비선형 MLP를 지나는 first 절반과, 그냥 나오는 second절반이 Additive coupling law로 합쳐지는 것을 볼 수 있습니다.

3. Experiments

3-1. Loglikelihood and Generation

실험은 다른 생성 모델과 마찬가지로 log likelihood( $log p_{X}(x)$ )를 관찰하였습니다. 실험 조건에 대해서 간단히 설명해 드리면 일단은 데이터의 dequantized version을 사용했다고 언급되어 있는데 이는 prior가 연속 확률 분포를 갖기 때문에 $p(x)$도 연속 확률 분포일 것이기 때문이라고 생각했습니다. 또한 whitening, ZCA 등의 전처리를 해주었는데 이는 각 차원이 uncorrelate하게 해주는 전처리 입니다. 첫번째 실험 결과는 다음과 같습니다.

사실 해당 표만 갖고는 별로 언급할 사항은 없습니다. 다른 모델과 비교한 것은 다음과 같습니다.

비교에 사용된 ‘Deep MFA’ 모델은 2012년의 density estimation 모델이고 ‘GRBM’은 restricted boltzmann machine 게열 모델입니다. 두개다 현시점에서는 오래된 모델들이기에 당시에 NICE가 기존 모델들에 비해서 꽤 괜찮은 성능을 보였다는 것만 확인하면 될 것 같습니다. 또한 당연하게도 아래 식과 같이 $h$를 샘플링한 후에 이미지를 생성해 낼수 있습니다.

NICE가 생성해낸 이미지는 다음과 같습니다.

다만 생성한 이미지 퀄리티가 그다지 좋아보이지는 않습니다.

3-2. Inpainting

제가 생성 모델쪽 많은 논문을 보지는 않았지만 본 논문에는 제가 읽었던 다른 논문에서는 없었던 재밌는 실험이 있습니다. 바로 이미지의 일부분을 가리거나 노이즈를 준 뒤 원본 이미지를 복원하는 실험입니다. 그 방법은 간단한데 이미지에서 정상으로 관찰된(노이즈는 주지 않은) 부분을 $x_{O}$ 노이즈를 준 부분을 $x_{H}$라고 합니다. 이때 학습되어 있는 NICE를 이용하여 $x_{H}$를 변수로 log likelihood 값을 최대화 하도록 학습하는 것 입니다. 식은 다음과 같으며 $\alpha$는 step size를 $i$는 iteration number를 의미합니다.

이러한 방법을 통해 일부분 관찰된 데이터가 들어왔을 때 노이즈가 존재하거나 관찰되지 않은 부분을 복원시킬 수 있습니다. 결과는 다음과 같습니다.

해당 결과로 부터 NICE가 한 데이터의 일부분의 차원 정보로 부터 $p(x)$를 잘 유추할 수 있으므로 데이터의 분포를 잘 학습하였다고 할 수 있습니다.

4. 추가 실험

4-1. Visualization of Scaling factor

본 논문은 추가적으로 데이터별로 $S_{ii}$를 크기별로 정렬하여 시각화하는 실험을 진행했습니다. 정확히는 $\sigma_{d} = S^{-1}_{dd}$ 를 크기별로 정렬하여 시각화하였습니다. y축은 $\sigma_{d}$, x축은 정렬 번호를 의미하며 결과는 다음과 같습니다.

$\sigma_{d}$가 크다는 것은 $S^{-1}_{dd}$가 작다는 것으로 해당 차원이 중요한 차원이라는 의미입니다. 그림을 보면 MNIST 데이터 셋에서 유독 $\sigma_{d}$들이 불균형한데 이는 MNIST 데이터 셋은 불필요한 배경이 많기 때문에 다른 데이터들 보다 상대적으로 필요한 차원, 불필요한 차원으로 구분이 되기가 쉽기 때문으로 유추하였습니다.

5. 다른 생성 모델들과의 비교

가장 대표적인 생성 모델은 크게 GAN, VAE, Normalizing Flow 계열 모델들 입니다. 본 목차에서는 3가지 모델들의 공통점 및 차이점을 아주 간략히 알아볼 수 있도록 하겠습니다. 3 모델은 학습 목표에 있어 가장 큰 차이점이 존재합니다. GAN은 특히 나머지 2 모델들과는 꽤 다른 학습 목표를 가지고 있습니다. 식없이 간단하게 표현하면 진짜 같은 데이터 샘플을 만들어내는 것이 목표입니다. 물론 이 과정에서 $p_{X}(x)$를 estimation 할 수 있고 이러한 estimation이 올바른 $p_{X}(x)$를 구하기를 기대하겠지만 본디 목적은 $p_{X}(x)$를 계산하거나 최대화하는 것은 아닙니다. 그러나 VAE, Normalizing flow 모델은 본디 목적이 $p_{X}(x)$를 최대화 하는 것 입니다. 다만 이 과정에서 아래와 같이 VAE는 $log p_{X}(x)$의 lower bound인 ELBO를 normalizing flow를 true log-likelihood 값을 최대화하는 것을 목적으로 합니다.

• Objective function of VAE: Maximize ELBO

VAE 모델은 ELBO를 최대화하기 위해 주로 sampling을 사용하며 이는 $p_{X}(x)$를 최대화 하는데 있어 bias로 작용할 수 있습니다. 하지만 NF 모델은 본질적으로 $p_{X}(x)$를 계산하는데 있어 bias가 전혀 없습니다. 대신 본 NICE 논문에서 보여드린 것 처럼 구현에 있어 엄청난 제약들이 존재하기 때문에 실제로 true $p_{X}(x)$를 계산하는 것은 쉬운일은 아닐 것이라 예상됩니다.

6. Future Work

NICE와 같은 flow-based 모델들의 방향은 대표적으로 다음과 같습니다.

• Determinant는 쉽게 구할 수 있지만 invertible $f(x)$ 구현하기

따라서 추후의 많은 논문들이 $f(x)$가 $p_{X}(x)$를 표현하기 충분한만큼 복잡한 함수로 만드는데 집중합니다. NICE 이후의 flow-based 모델중 한가지인 realNVP는 아래 사진과 같이 데이터를 조금 더 복잡하게 분해하는 ‘masked convolution layer’와 additive coupling layer보다 복잡한 연산을 가능케 하는 ‘combining coupling layers’를 구현하여 좀 더 표현력있는 $p_X(x)$를 계산하였습니다.

또한 realNVP 이후 모델인 GLOW는 invertible한 1x1 convolution을 사용하여 데이터 분해시 permutation을 일반화 하면서 성능 향상을 일으켰습니다. Flow++ 모델은 다른 dequantization 방법을 적용하고 일반적인 coupling layer보다 훨씬 복잡한 연산을 보장하는 logistic mixture CDF coupling layer를 도입함으로서 다시 한번 성능 향상을 일으켰습니다. 이와 같이 NICE 이후의 flow-based model들은 determinant는 쉽게 구할 수 있지만 invertible $f(x)$ 구현하는데 많은 초점이 맞춰져 있는 것을 알 수 있습니다.