WGAN

Introduction

WGAN 이란? 적대적 신경 생성망 GAN의 비용함수를 Wasserstein distance로 설정하여 최적화를 진행하는 신경망이다.

기존의 GAN은 이미지가 복잡해 짐(고차원화) 에 따라 학습의 난이도가 아주 올라가게 되고 이로 인해 학습이 매우 불안정 해지는 문제가 발생하게 되었다.
WGAN에서는 학습의 불안정성의 원인을 metric(거리)이라 보고 이것을 수학적으로 해결하고자 하였다.

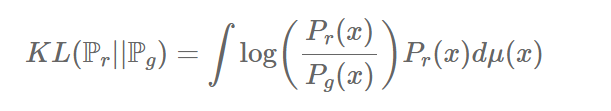
Untitled
[출처] Original Paper [1]
기존의 두 분포 사이의 거리를 측정하기 위해 주로 쓰이는 KLD는 위수식과 같다.
하지만 KLD와 같은 metric은 분모에 위치하는 $P_g(x) = 0$ 이고, $P_r(x) \ne 0$ 인 곳이 발생하게 된다면 발산하게 되는 문제점이 생긴다.
본 논문에서는 저차원에서 주로 이러한 문제가 발생한다고 서술하고 있다.

Untitled
[출처] deeplearning.ai “Build Basic Generative Adversarial Networks (GANs)” 강의자료[3]
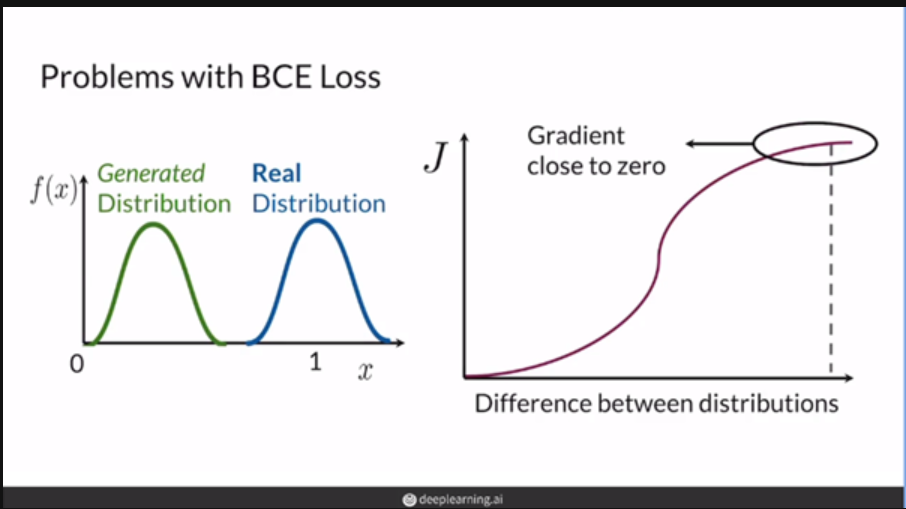
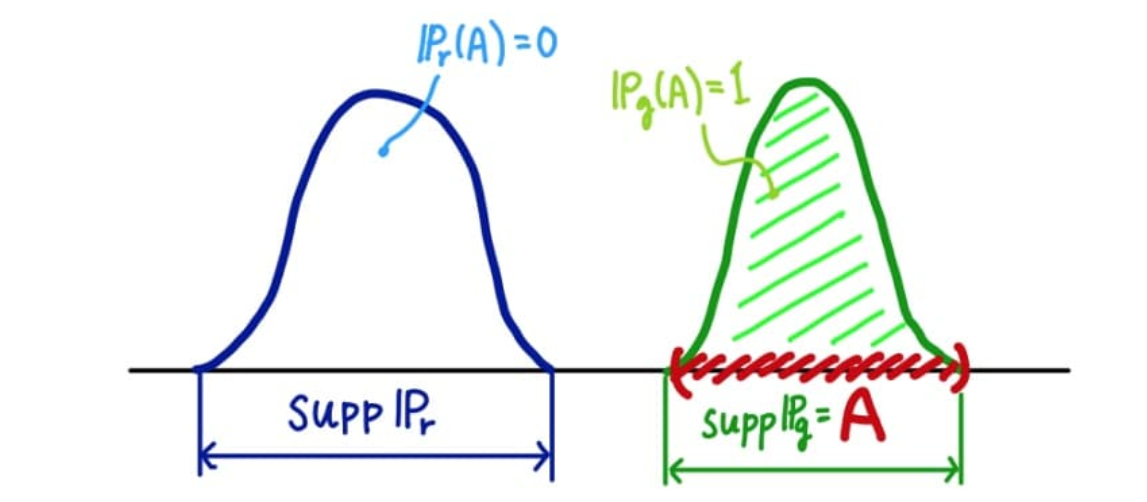
또한 위 그림과 두 분포가 겹치지 않는 다면, 즉 support가 겹치지 않은 상황에서 역시 두 분포 사이의 거리가 상당히 멀어 좋지 않은 gradient feedback을 주게 되고 유의미한 학습이 일어나기가 힘들다 는 문제가 있다.

따라서 본 논문에서는 모델의 학습이 얌전히 수렴하고, 매끄러운 metric을 찾는 것을 목표로 한다.

Different Distances


본 섹션에서는 어떤 metric이 더 GAN의 학습에 적절한 한지 알아보기 위해 논문에서 다루고있는 다양한 Distance 를 구하는 방법들과 해당 방법이 가지고 있는 문제점을 살펴본다.

The Total Variation(TV) Distance


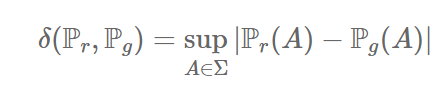
Untitled
[출처] Original Paper [1]

위의 식은 Total Variation (TV) distance를 나타낸다. 여기서 $sup$ 은 supremum 최소상한라는 의미이며 어떤 집합의 상한 중 가장 작은 값을 의미한다.

TVD는 두확률 분포의 가능한 측정 값들 중 차이가 가장 큰 값 $sup$ 으로 정의된다.

Untitled
[출처] Wasserstein GAN 수학이해하기 [2]

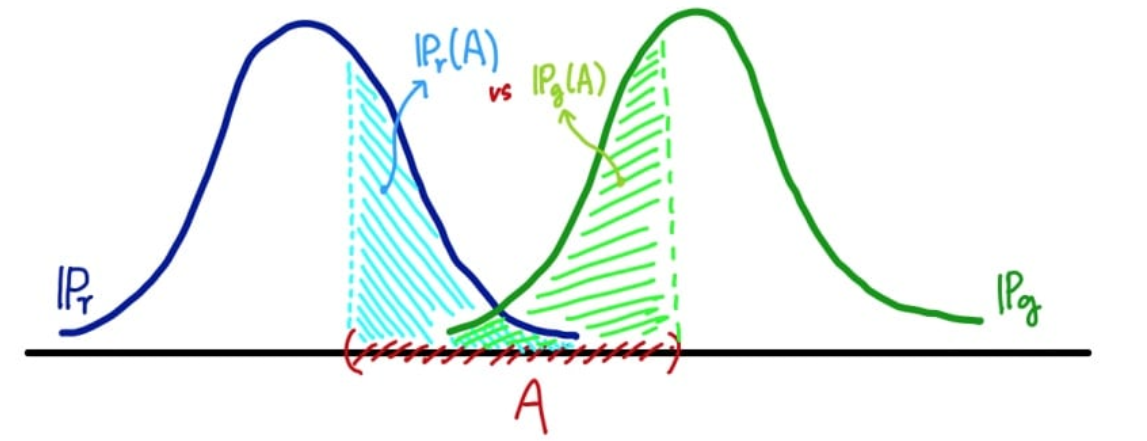
위 그림에서 처럼, 가능한 사건들을 A로 잡았을 때, 두 분포를 비교 했을떄 측정 값은 서로 다른값을 가지게 된다. 따라서 두 분포중 큰 값을 TVD로 한다.

Untitled [출처] Wasserstein GAN 수학이해하기 [2]

TVD 에서 만약 두 분포가 겹치지 않는다면 즉 support가 공집합이라면, TVD는 1을 가지게 된다.

The Kullback-Leibler Divergence


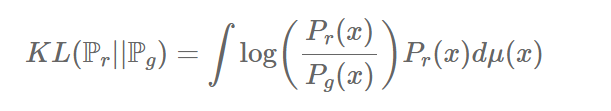Untitled [출처] Original Paper [1]
위에서 언급 했던 대로 KLD은 분모에 위치하는 $P_g(x) = 0$ 이고, $P_r(x) \ne 0$ 인 곳이 발생하게 된다면 발산하게 되는 문제점이 생긴다.

The Jensen-Shannon Divergence


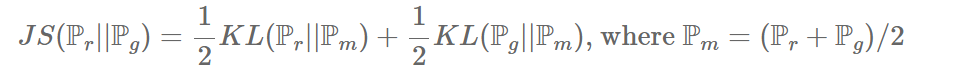
Untitled
[출처] Original Paper [1]

JSD는 KLD를 이용하여 간략하게 표현 될 수 있다.
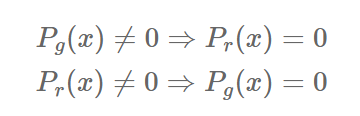
만약 두 분포의 support 가 겹치지 않는다면 Untitled
[출처] Original Paper [1]
으로 나타나게 되고
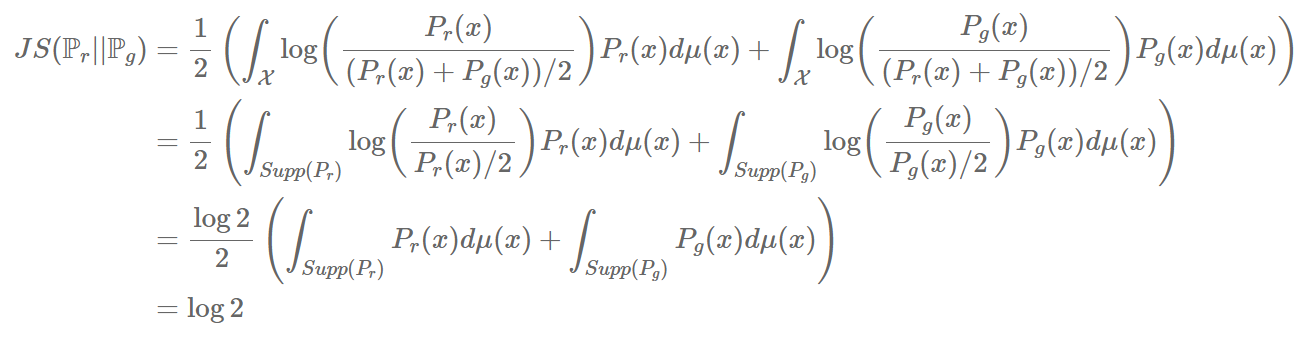
Untitled
[출처] 블로그 포스팅 [4]

위 수식처럼 $log2$ 로 두 분포사이의 거리가 고정된다. 따라서 JSD는 발산하지는 않지만 $log2$ 처럼 상수 값만 가지게 되므로 좋은 피드백을 주는 것이 어렵다.

The Earth Mover (EM) Distance (Wasserstein-1)


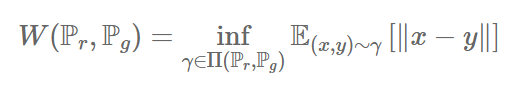
Untitled
[출처] Original Paper [1]

위 식은 EMD 즉 Wasserstein 을 보여준다.
EM은 $P_r$ 을 $P_g$ 로 변경하기 위한 여러 경우 중 가장 최적의 transform plan에 대한 cost를 구할 수 있도록 해준다.

EM의 타당성 설명


Untitled
[출처] Original Paper [1]

본 논문에서는 위에서 논의한 다양한 distance 들과 EM을 비교하여 EM의 타당성을 이야기한다. 기존의 GAN 논문에서 Disciminator 와 Gnerator가 학습할 떄 EM을 제외한 다른 metric을 사용한다면,
$\theta \ne 0$ 일 경우 두 분포가 겹치지 않게 되고 무의미한 값들을 구하게 된다.
하지만 EM의 경우 공식에 따라 두 점사이의 거리는 항상 $\left\vert \theta \right\vert$ 로 나타나게된다.

Untitled
[출처] Original Paper [1]

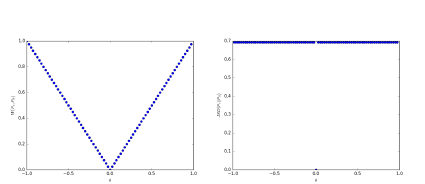
위 그림은 논문에서 JSD와 EM의 gradient를 비교하여 보여주는 그림이다.
오른쪽의 그림은 JSD를 보여주는데 JSD의 경우 $\theta = 0$ 이외에선 상수로 일정하게 나타나고,
$0$ 일 떄는 $0$ 으로 나타나게 된다. 따라서 유의미한 gradient를 얻기가 힘든 것을 알 수 있다.
왼쪽 첫번 째 그림의 EM의 경우 좀 더 유의미한 gradient를 내보내는 것을 볼 수 있다. 따라서 EM 즉 W distance가 GAN의 학습에 좀더 유용하다는 것을 알 수 있다.

Wasserstein GAN


본 논문에서는 Wasserstein 1 Distance를 GAN의 Loss function으로 정의 했다.
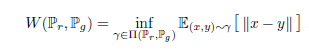
Untitled
[출처] Original Paper [1]

의 EM 공식을 살펴보면 inf가 나오는 해당 부분의 계산이 intractable 하다.
따라서 논문에서는 Kantorovich-Rubinstein duality를 사용하여 식을 변경한다.
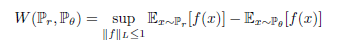Untitled [출처] Original Paper [1]

이렇게 식을 정리하게 되면 위 수식과 같이된다.
위 수식에서 $\left\vert\left\vert f \right\vert\right\vert_L \leq 1$은 $f$ 가 1-립쉬츠 함수,
즉 임의의 두점 사이의 평균변화율이 1이 넘지 않는 함수 라는 뜻을 의미한다.
위의 정리된 수식을 사용하면 $f$ 만 알아 낼 수 있다면 $W$ 값을 얻을 수 있다.

본 논문에서는 $w$를 추가로 변수로 사용하여 $f_w$ 를 업데이트 하고 있다.
기존 위의 수식에서 $P_\theta$ 를 $g\theta(z)$ 로 바꾸어 주면 아래 수식과 같은 식이 나온다.

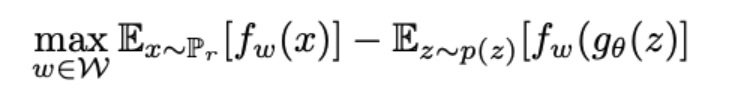
Untitled
[출처] Original Paper [1]

위의 수식의 모양이 GAN의 Loss 함수와 비슷한 모습을 보이는 것을 알 수 있다.

본 논문에선 립시츠 조건을 만족하도록 discriminator (Critic)의 파라미터 W가 일정범위 [-0.01, 0.01] 내에 있도록 강제로 제한한다.
이과정을 clipping이라고 부른다. 이 방법에 대해서 논문에선 cleary terrible way 라고할 정도로 좋지 않게 표현하고 있다. 하지만 실험 결과 해당 방법이 너무 간결하고 좋은 결과를 보여 사용했다고 언급하고 있다.

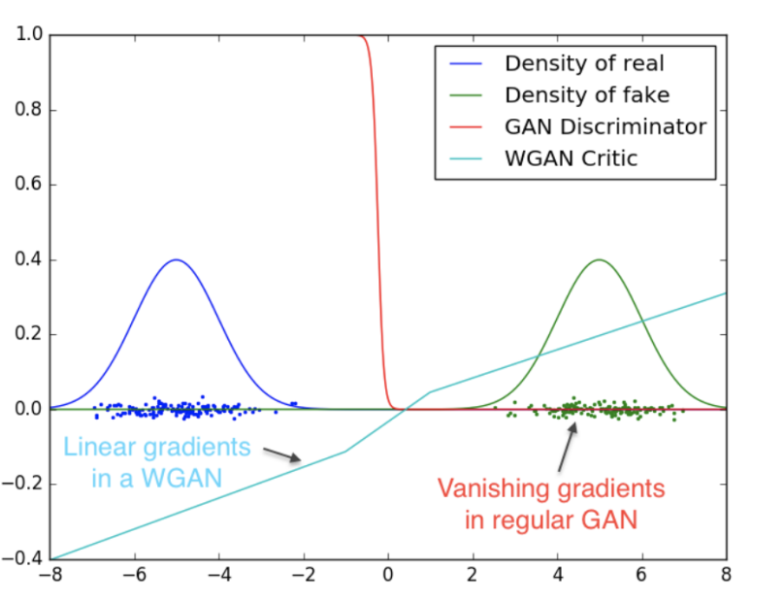
Untitled
[출처] Original Paper [1]

위 그림에서는 기존 GAN과 WGAN의 discriminator (Critic)이 어떻게 다르게 동작하는지 보여준다.
그림에서 빨간색은 GAN의 discriminator를 나타내는데, 빠르게 fake와 real을 잘 구분할 수 있게 되지만 discriminator가 결국 gradient vanishing이 발생하게 된다.
하지만 하늘색 선의 WGAN의 경우 critic이 gradient vanishing에 빠지지 않고 linear 하게 gradient가 잘 발생된다.
따라서 model collapse가 발생할 수 없는 상황이 된다.

Code

Critc code

아래 코드는 WGAN의 Crtic의 학습 코드를 보여준다.


for ix in n_critic_steps:
  opt_critic.zero_grad()

  real_images = data[0].float().to(device)

  # * Generate images
  noise = sample_noise()
  fake_images = netG(noise)

  # * though they are name so, they are not logits!
  real_logits = netCritic(real_images)
  fake_logits = netCritic(fake_images)

  # * max E_{x~P_X}[C(x)] - E_{Z~P_Z}[C(g(z))]
  loss = -(real_logits.mean() - fake_logits.mean())

  loss.backward(retain_graph=True)
  opt_critic.step()

  # * Gradient clippling
  for p in netCritic.parameters():
      p.data.clamp_(-0.01, 0.01)

코드를 확인해 보면 논문에서 제안한 아이디어와 같이 노이즈를 생성하고
해당 노이즈를 이용하여 가짜 이미지를 생성한 후 가짜 이미지와 진짜 이미지간의 차이를
위에서 제시한 loss 함수를 구하고 구한 Critic parameter들을 [-0.01, 0.01] 범위로 강제로 clipping 한다.

WGAN Gnerator Code

아래의 코드는 WGAN의 코드를 보여준다. 논문에서 제안하는 loss 함수를 사용하여 다음과 같이 구현할 수 있다.


opt_gen.zero_grad()

noise = sample_noise()

fake_images = netG(noise)

# again, these are not logits.
fake_logits = netCritic(fake_images)

# * - E_{Z~P_Z}[C(g(z))]
loss = -fake_logits.mean().view(-1)

loss.backward()
opt_gen.step()

Empirical Results


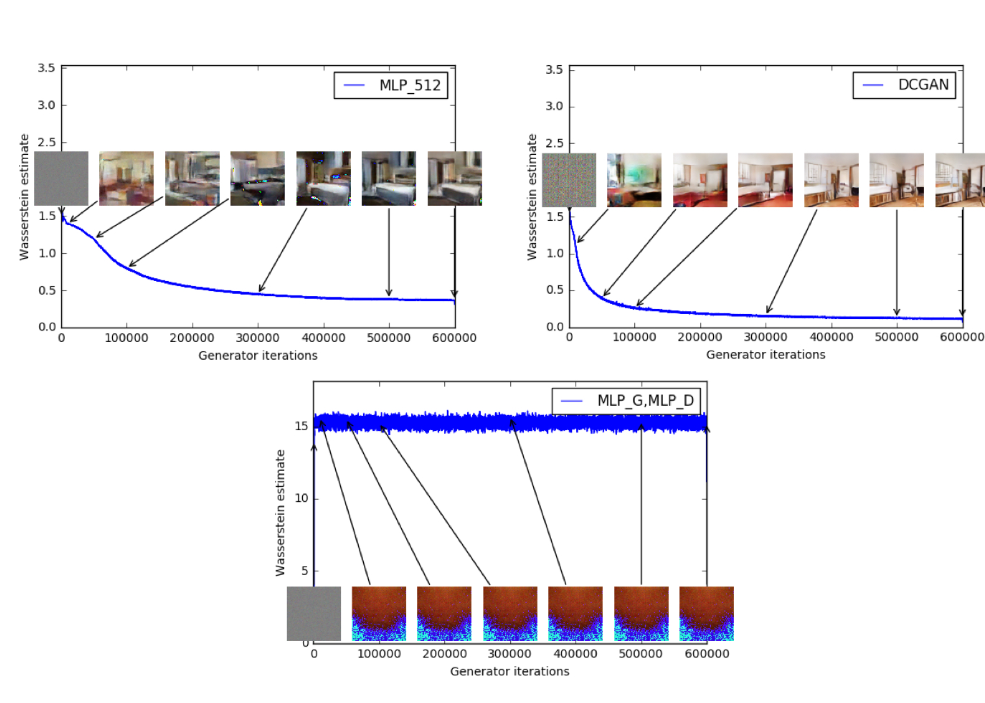Untitled [출처] Original Paper [1]
위 그림은 EMD를 사용하여 학습을 진행할 때 나오는 이미지와 estimation 간의 상관관계를 보여준다.
그림을 살펴보면 W 값은 이미지의 퀄리티가 좋아 질 수록 W가 점점 감소하는 것을 볼수 있고, 마지막 사진에선 망가진 이미지가 나올 때는 W가 줄어들지 않는 모습을 보인다.

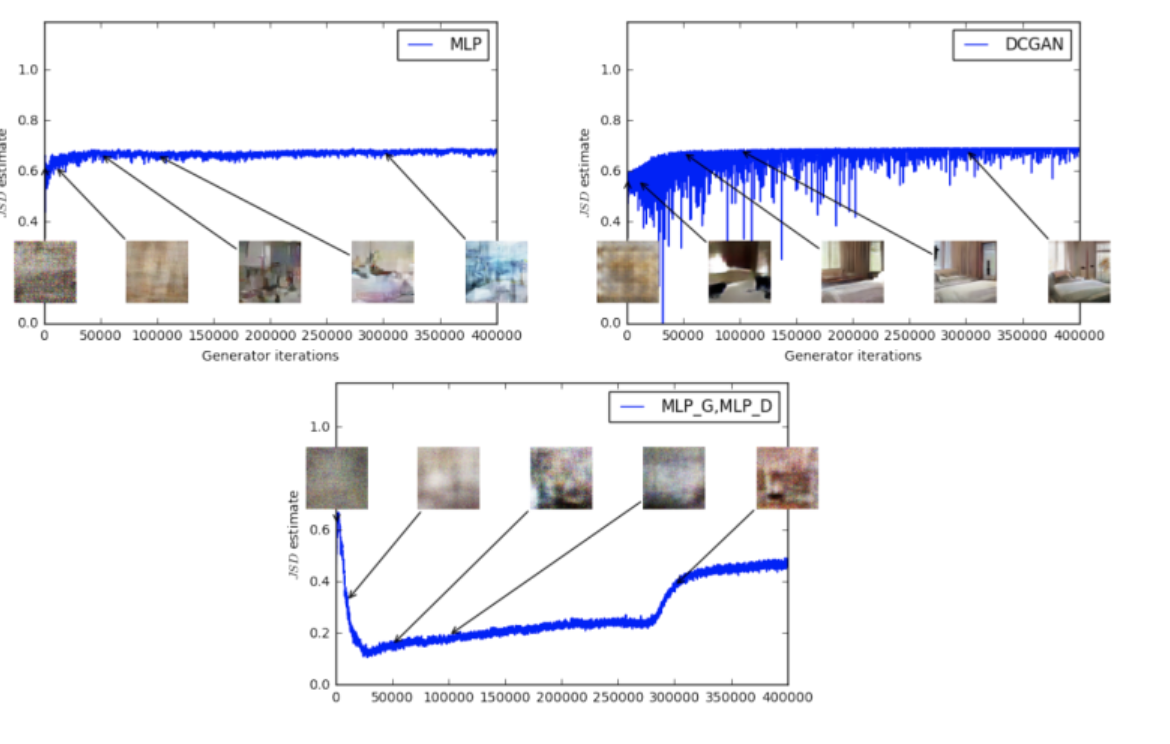
Untitled [출처] Original Paper [1]
위 그림은 JSD를 사용하여 학습을 진행항 때 나오는 이미지와 estimation 간의 상관관계를 보여준다.
JSD의 같은 경우 이미지의 품질에 상관없이 estimation이 $log2$ 즉 약 0.69로 고정되는 모습을 보인다.
또한 마지막 망가진 이미지의 사진에선 오히려 내려갔다 올라가는 모습을 보이기도한다.

Improved stability


WGAN의 장점 중 하나는 critic을 최적까지 학습하도록 한다는 것이다.
이에 따라, 논문에서는 WGAN을 사용할 때 generator와 discriminator의 capacity를 적절하게 균형 맞출 필요가 없다고 말하고 있다.
또한 critic이 더 좋을 수록 더 좋은 퀄리티의 gradient로 generator를 학습 시킬 수 있다고 한다.
논문에서는 WGAN의 stability를 확인하기 위해 3가지 generator 구조에서 실험을 진행했다.

  1. Convolutional DCGAN generator
  2. Convolutional DCGAN generator without batch normalization
  3. 4-layer RelU-MLP hidden units

여기서 WGAN과 GAN discriminator를 위해 convolutional DCGAN 구조를 사용했다.

Untitled [출처] Original Paper [1]

위 그림은 각 경우에 generator에서 생성한 샘플들의 그림을 보여준다.
맨 위의 Figure 5은 위에서 설명한 첫번 째구조 즉, convolutional DCGAN generator에서 생성된 그림은 보여분다. 그림 중 왼쪽 그림은 WGAN에서 생성된 그림이고, 오른쪽은 standard GAN에서 생성된 그림이다. 해당 그림에선 WGAN과 GAN 모두 high quality의 그림샘플을 잘 생성하는 것을 볼 수 있다.

위 그림 중 Figure6 에서는 convolutional DGAN without batch nomalization의 경우에 생성된 그림을 보여준다. 왼쪽은 WGAN, 오른쪽은 standard GAN에 의해 생성된 샘플을 보여준다. 그림의 결과에서 알 수 있듯이 WGAN의 경우 이미지를 잘 생성하지만,standard GAN의 경우 이미지 생성에 실패한 것을 알 수 있다.

마지막으로 위 그림 중 Figure 7 에선 MLP generator 와 4-layer and 512 unit 그리고 ReLU를 사용한 경우를 보여준다. 그림에서 왼쪽은 WGAN 오른쪽은 standard GAN의 생성 결과를 보여준다. WGAN의 경우 DCGAN보다는 퀄리티가 낮지만 그래도 여전히 어느정도 완성된 샘플들을 생성하고 있으나, standard GAN의 경우 낮은 퀄리티의 이미지를 생성할 뿐더러 지속해서 같은 이미지를 생성해 내는 mode collapse가 발생한 것을 볼 수있다.

이를 통해 WGAN를 사용한 경우 model coallapse가 잘 발생하지 않는 것을 확인 할 수 있으며, 기존의 GAN에 비해 더 안정적으로 이미지를 생성할 수 있음을 확인 할 수 있다.

Untitled [출처] Original Paper [1]

추가적으로 확인 하기 위해 마지막 3번 째 경우 WGAN 에서 생성된 데이터를 살펴 보아도 아래 그림의 standard GAN에서 생성된 이미지들에 비해 mode collapse가 확인되지 않는 것을 볼 수 있다.

Untitled [출처] Original Paper [1]

Conclusion


해당 논문에서는 dicriminator와 Generator 간의 균형을 유지하며 학습하기 어려운
GAN이 가진 문제점을 해결하기 위해 Discriminator 대신 새로운 Critic을 정의하여 사용하며, Critc을 구하기 위해 Wasserstein distance (EMD)를 사용한다.
EMD를 통해 GAN에서 주로 발생하는 문제인 mode collapse를 해결 하고 있다는 점에서 인상적이다. 하지만 본 논문에선 립시츠 조건을 만족하기 위해 weight clipping 방법을 사용하고 있는데, 해당 법이 좋지 않음에도 사용하고, 추후에 어떻게 개선시켜야 할지에 대해 논의하고 있지 않는 점이 아쉽다고 생각된다.

Future Work


WGAN에서 Wasserstein distance는 모든 데이터 결합 분포간의 최소 cost를 구하기 위해 K-립쉬츠 continuous를 사용한다. 즉 모든 점에서 연속적으로 미분이 가능하게 하여 기울기 계산이 가능하게 하기 위해선 $\left\vert\left\vert f \right\vert\right\vert_L \leq 1 $ 과 같은 조건을 만족해야한다. 해당 조건은 모든 (x1, x2)에 대해서 $ \left\vert f(x1) - f(x2)\right\vert \leq K \left\vert x1 -x2 \right\vert $ 의 식을 만족해야함을 의미한다.
이 립쉬츠 조건을 만족하기 위해 본 논문에선 [-0.01, 0.01] 로 gradient를 cliping 하고 있다. 이에 따라 학습의 결과 -0.01 or 0.01 분포가 몰려 있는 문제가 나타나게 된다. 이릴 해결하고자 Gradient penalty를 추가한 WGAN-GP [5]를 제안한다.

Reference


[1] Wasserstein GAN

[2] https://www.slideshare.net/ssuser7e10e4/wasserstein-gan-i

[3] deeplearning.ai “Build Basic Generative Adversarial Networks (GANs)” 강의자료

[4] https://haawron.tistory.com/217

[5] Improved Training of Wasserstein GANs

https://velog.io/@sjinu/Metric-for-WGAN

https://indigopyj.github.io/wgan/