WGAN-GP

Improved Training of Wasserstein GANs

Untitled

Background

GAN

GAN은 Generator와 Discriminator의 minmax경쟁에서 Disciminator가 매 step에서 optimal 일 때 경쟁은 수렴하며 이때 Generator가 생성하는 데이터의 분포는 training data의 분포와 동일하게 됨을 증명하면서 특정 모델 구조에 제약을 받지 않는 강력한 생성모델의 가능성을 보여주었습니다. 이는 VAE와 normalize flow 모델이 architecture 상의 제약 조건(flow모델의 경우 역함수가 존재해야하며, VAE의 경우 sampling에서 자유로울 수 없다)이 존재하는 것과 대비되는 것을 알 수 있습니다.

\[\begin{align} V(G,D^*) &= E_{x \sim p_{data} (x)} [ \log(D^{*}(x)) ] + E_{x \sim p_{g} (x)} [ \log(1-D^{*}(x)) ]\\ &= - \log(4) + \text{KL} (p_{data} \Vert \frac{p_{data} + p_{g}}{2}) + \text{KL} (p_{g} \Vert \frac{p_{data} + p_{g}}{2})\\ &= - \log(4) + 2 \times \text{JSD}(p_{data} \Vert p_{g}) \end{align}\]

WGAN

기존의 GAN 처럼 Jensen-Shannon Divergence 최소화하는 방식은 vanishing gradients가 발생할 수 있습니다. generator의 파라미터에 의해 잠재적으로 불연속이($p_g$ 의 support가 $p_{data}$ 와 전혀 겹치지 않는 경우 즉, sampling된 이미지 x가 반대편의 분포에서 나올 확률이 0이 되면 Jensen-Shannon Divergence는 일정한 상수값이 됩니다.) 될 수 있는 Jensen-Shannon Divergence 대신에 WGAN에서는 대안으로 Wasserstein-1 distance를 제시하였습니다.

Untitled

Wasserstein-1 distance

Earth-Mover라고도 불리는 Wasserstein-1 distance는 다음과 같이 정의 됩니다.

\[W(p_r,p_g)=\inf_{\gamma \sim \Pi(p_r,p_g)}\mathbb{E}_{(x,y) \sim \gamma}[ \Vert x-y \Vert ]\]

즉, $p_g$ 를 $p_{r}$ 로 변형하기 위한 transporting mass의 최소 비용(하한)으로 정의됩니다.

Kantorovich-Rubenstein duality를 이용하여 Wasserstein-1 distance를 value function로 표현하면 아래와 같습니다.

\[\min_G\max_{D\in \mathcal{D}}\mathbb{E}_{x \sim \mathbb{P}_r}[D(x)]-\mathbb{E}_{\tilde x \sim \mathbb{P}_g}[D(\tilde x)]\]

$\mathcal{D}$ 는 1-Lipschitz functions이며 $\mathbb{P}_g$ 는 $\tilde x \sim G(z), z \sim p(z)$ 로 정의됩니다. (GAN은 확률분포 $p$ 에 대해 제약이 없어서 무엇이든 상관없다) optimal Discriminator가 주어졌을 때 WGAN의 value function을 generator에 대해 최소화하는 것은 $W\left(\mathbb{P}{r}, \mathbb{P}{g}\right)$ 를 최소화 하는 것과 같습니다.

WGAN의 value function을 사용할 때 Discriminator가 1-Lipschitz functions 이어야 한다는 조건이 생겼죠. WGAN에서는 Discriminator(WGAN에서는 critic이라고 부른다)의 weights set이 [-c,c]범위를 갖도록 제한하여 이 조건을 만족시켰습니다. c는 critic의 architecture에 의존하기 때문에 모델이 바뀌면 실험을 통해 다시 찾아야하는 수고로움도 있고 여러 문제를 일으킵니다. (https://www.geogebra.org/calculator/sxfwerg8)링크에서 모델을 변형하고 적절한 c를 찾아보세요.

놓치기 쉬운 부분인데, Discriminator가 1-Lipschitz functions이라는 것은 기울기가 -1~1이라는 것이죠. 그럼 무엇에 대한 기울기일까요? 바로 $x$에 대한 기울기 입니다. 자세한 이유는 Kantorovich-Rubenstein duality을 찾아보시면 좋을 것 같습니다. 아무튼 gradient penalty에서의 gradient도 $\hat{x}$에 대한 기울기를 의미합니다. optimal critic의 기울기가 1이라는 말은 critic이 optimal이면 생성된 이미지 $x$가 실제 이미지 $y$방향으로 $t$만큼 가까워지면 $t$만큼 가까워진 거리가 되도록 해야한다는 것이죠.

WGAN의 알고리즘은 실제로 아래와 같이 구현 됩니다. c는 0.01인데 실험을 통해 구했다고 합니다.

Untitled

언어모델(Language Model)

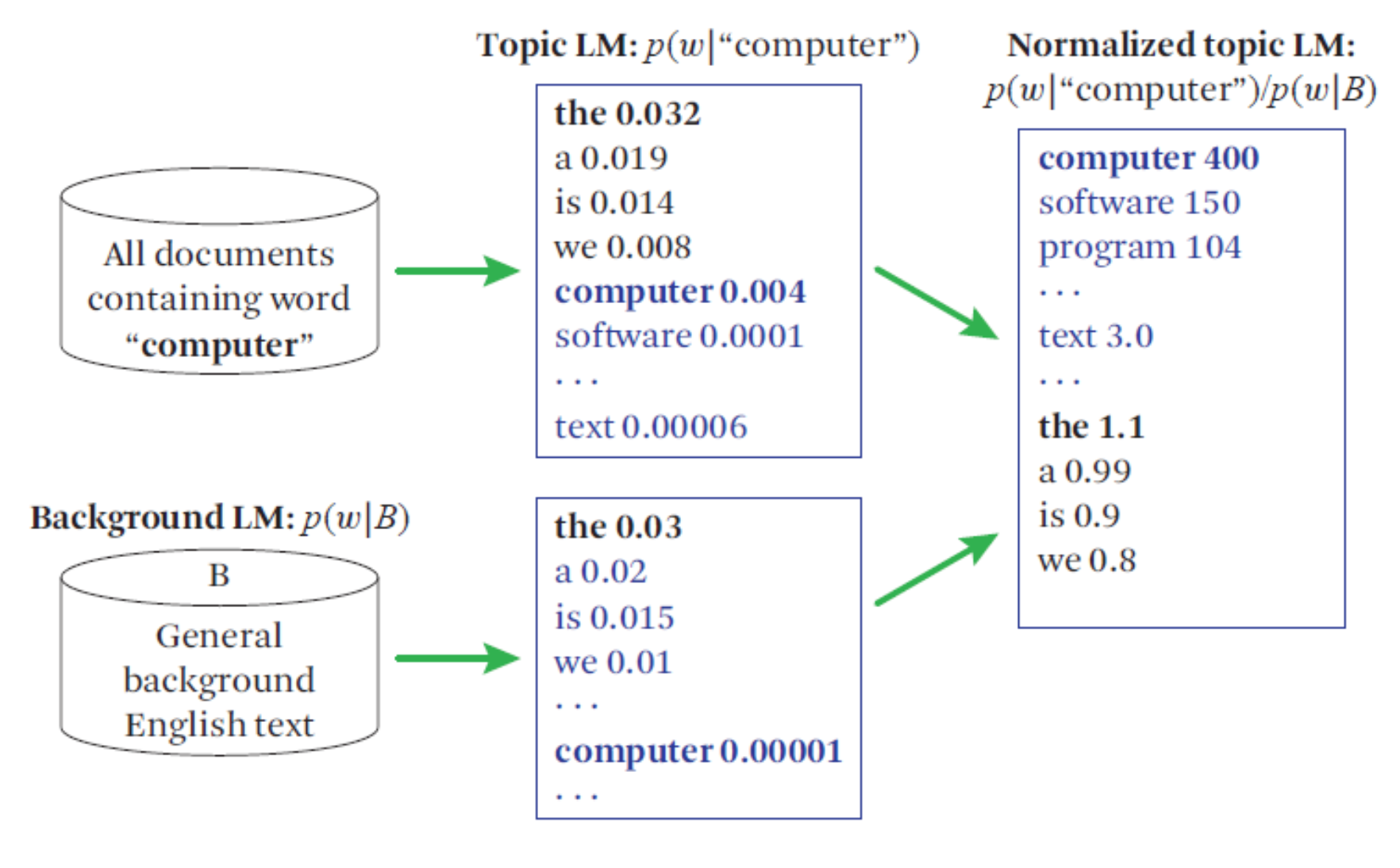
Untitled

대부분의 언어모델은 단어단위로 문장을 생성합니다. 문장을 생성하는데 단어단위로 충분하기도 하고 GAN을 이용할때 문자단위로 생성하게되면 discriminator가 판단하기 너무 쉽습니다. 특히 GAN는 discriminator가 saturation되는 것에 취약하기 때문에 어려운 일입니다.

Abstract

WGAN-GP에서는 WGAN에서 1-Lipschitz constraint를 만족시키기 위해 사용한 weight clipping이 좋지 않음을 보이고 loss에 gradient penalty 부과하여 1-Lipschitz constraint를 만족시키는 것을 제안합니다.

Contributions

논문의 Contributions는 다음과 같습니다.

Toy datasets에 대해 critic의 weight clipping이 undesired behavior를 유발할 수 있다는 것을 증명한다.
“Gradient penalty”(WGAN-GP)를 제안하고 이를 이용하여 weight clipping로 인한 문제를 해결한다.
다양한 GAN 구조에 대해 안정적인 학습이 가능함을 보인다, weigth clipping에 대한 성능 향상, 고품질 이미지 생성, 문자 수준의 GAN 언어모델을 선보인다.

Properties of the optimal WGAN critic

weight clipping의 문제점을 밝히고 gradient penalty의 필요성을 설명하기 위해 optimal WGAN critic에 대해 짚고 넘어가겠습니다.

Untitled

compact metric space $\mathcal{X}$ 상의 두 분포 $\mathbb{P}_{r}$ 와 $\mathbb{P}_{g}$ 가 있을 때,1-Lipschitz function $f^*$ 가 $\max_{ \Vert f \Vert _L \leq 1 }\mathbb{E}_{y \sim \mathbb{P}_r}[f(y)]-\mathbb{E}_{x \sim \mathbb{P}_g}[f( x)]$ 의 optimal solution 이라고 하자.$\Pi(\mathbb{P}_r,\mathbb{P}_g)$ 을 두 분포의 결합분포들의 집합이라고 두고 $W(\mathbb{P}_r,\mathbb{P}_g)=\inf_{\pi \sim \Pi(\mathbb{P}_r,\mathbb{P}_g)}\mathbb{E}_{(x,y) \sim \pi}[ \Vert x-y \Vert ]$ 의 optimal coupling $\pi$ 이 있다고 할 때, $f^*$ 가 미분가능하고 $\pi(x=y)=0$ 을 만족하면 $x_t=tx+(1-t)y \text{ with } 0 \leq t \leq 1$ 일때 $\mathbb{P}_{(x,y) \sim \pi}[\nabla f^*(x_t)=\frac{y-x_t}{ \Vert y-x_t \Vert }]=1$ 를 만족한다. 따름정리: $\mathbb{P}_{r}$, $\mathbb{P}_{g}$ 에서 $f^*$ 의 gradient의 크기는 거의 대부분 1이다.

뒤에서 이러한 특징을 이용하여 Gradient penalty를 부여합니다.

Difficulties with weight constraints

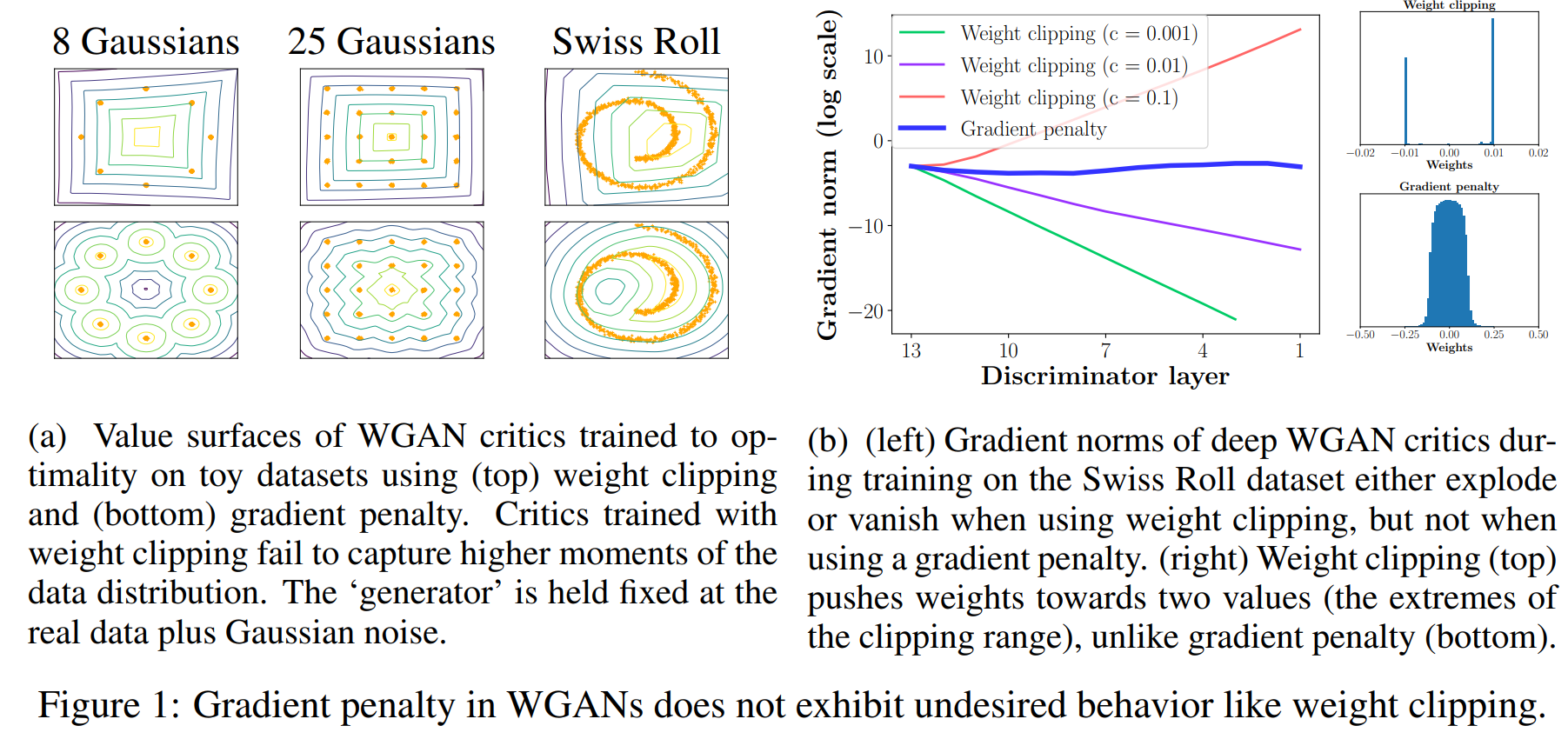
Untitled

가중치에 제약조건을 다는 것이 학습에 좋지 않은 영향을 끼친다는 것을 보여주는 실험입니다. 왼쪽의 실험은 WGAN에 weight clipping을 적용한 것(위) 과 Gradient penalty를 적용한 것(아래)를 비교한 실험입니다.

그래프에서 볼 수 있듯이 weight clipping을 적용하면 뒤쪽 layer로 갈수록 gradient의 크기가 기하급수적으로 커지는 것을 확인할 수 있을 것입니다. 반면 gradient penalty를 적용한 경우 gradient의 크기가 model의 전반에 걸쳐서 대부분 일정한 것을 확인할 수 있습니다.

DNN모델에서 gradient가 매우 크다는 것은 좋지 않습니다. weight clipping을 적용하면 gradient가 매우 커도 weight의 크기가 제한되므로 범위의 양 극단에 쏠리겠지요. 이 또한 DNN에서 피해야 하는 상황입니다.

논문에서는 weight clipping대신 gradient penalty를 적용하면 위에서 이야기한 두 가지 문제를 잡을 수 있기 때문에 gradient penalty를 사용하는 것이 좋다는 주장을 합니다.

Capacity underuse

weight clipping을 적용하여 k-Lipshitz constraint를 구현하면 critics가 단순한 함수로 편향된다고 합니다. Figure1의 그림 a는 최적의 clipping range를 찾아 학습시킨 것임에도 불구하고 Gradient penalty에 비해 상당히 단순한 value surface를 보여줍니다.

Gradient penalty

WGAN-GP는 이러한 문제를 근본적으로 접근합니다. 1-Lipshitz function논문에서는 직접적으로 critic의 gradient 크기(norm)에 대한 제약조건을 loss함수에 반영합니다.

항상 미분가능 함수의 gradient의 크기(norm)가 거의 어디서나(almost everywhere) 1이라는 것은 1-Lipshitz function이기 위한 필요충분조건입니다. 논문에서는 이 조건을 soft version으로 부여하기 위해 $\hat{x}\sim\mathbb{P}_{\hat{x}}$ 에서 sampling하여 penalty로 부여합니다.

\[L=\underbrace{\mathbb{E}_{\tilde x \sim \mathbb{P}_g}[D(\tilde x)]-\mathbb{E}_{x \sim \mathbb{P}_r}[D(x)]}_{\text{WGAN의 critic loss}}+\underbrace{\lambda\mathbb{E}_{\hat{x}\sim\mathbb{P}_{\hat{x}}}[( \Vert \nabla_{\hat{x}} D(\hat{x}) \Vert _2-1)^2]}_{\text{논문에서 제안하는 gradient penalty}}\]

최적화 문제에서 soft version of the constraint이라는 말은 제약조건을 만족하는 것을 objective function에 반영하여 제약조건을 만족하는 것도 하나의 목표로 하겠다는 것입니다.

학습과정에서 제약조건을 어기더라도 penalty를 부여하여 다시 돌아오도록 한다고 보셔도 좋을 것 같습니다

반면에 hard version of the constraint의 예로 weight clipping을 들 수 있습니다. 어떠한 상황에서도 weight가 특정범위에 있도록 clipping 하여 강제합니다.

constraint로 주어진게 optimal critic이기 위한 필요조건이라서 1보다 작은 경우는 critic이 아직 optimal 이 아니라고 보면 되는 것이고, constraint와 크게 벗어나서 립시츠 조건을 만족하지 못하는 상황에서는 critic의 출력값을 Wasserstein-1 distance계산에 사용하는 의미가 없어진다고 보시면 될 것 같습니다.

Gradient penalty는 아래와 같이 구현 됩니다.

def _gradient_penalty(self, real_data, generated_data):
	batch_size = real_data.size()[0]

  # Calculate interpolation
  alpha = torch.rand(batch_size, 1, 1, 1)
  alpha = alpha.expand_as(real_data)
  if self.use_cuda:
      alpha = alpha.cuda()
  interpolated = alpha * real_data.data + (1 - alpha) * generated_data.data
  interpolated = Variable(interpolated, requires_grad=True)
  if self.use_cuda:
      interpolated = interpolated.cuda()
  # Calculate probability of interpolated examples
  prob_interpolated = self.D(interpolated)
  # Calculate gradients of probabilities with respect to examples
  gradients = torch_grad(outputs=prob_interpolated, inputs=interpolated,
                         grad_outputs=torch.ones(prob_interpolated.size()).cuda() if self.use_cuda else torch.ones(
                         prob_interpolated.size()),
                         create_graph=True, retain_graph=True)[0] # 여기서보면 x에 대해서 미분하는 것을 확인핳 수 있습니다!!
  # Gradients have shape (batch_size, num_channels, img_width, img_height),
  # so flatten to easily take norm per example in batch
  gradients = gradients.view(batch_size, -1)
  self.losses['gradient_norm'].append(gradients.norm(2, dim=1).mean().data[0])
  # Derivatives of the gradient close to 0 can cause problems because of
  # the square root, so manually calculate norm and add epsilon
  gradients_norm = torch.sqrt(torch.sum(gradients ** 2, dim=1) + 1e-12)
  # Return gradient penalty
  return self.gp_weight * ((gradients_norm - 1) ** 2).mean()

Sampling distribution

Penalty coefficient

실험을 통해 $\lambda=10$ 이 다양한 모델과 데이터 세트에서 잘 작동하는 것을 확인했습니다.

No critic batch normalization

기존에 제안된 GANs에서는 generator & discriminator 모두에 batch normalization을 사용하여 학습을 안정화 시키는데 도움을 주려했습니다. 하지만 batch normalization을 사용하면 discriminator는 개별적 mapping에서 batch단위의 mapping으로 변하게 됩니다. 따라서 본 논문처럼 전체 배치에 대해서가 아니라 각 입력에 독립적으로 critic의 gradient norm에 대한 penalty를 줘야하는 상황에서 batch normalization는 더 이상 유효하지 않습니다. 이를 해결하기 위해서, 간단하게 모델 내의 critic에서 batch normalization을 생략합니다. batch normalization의 대안으로 layer normalization을 추천했습니다.

Two-sided penalty

논문에서는 gradient의 norm이 1 아래에 머무르기(one-sided penalty) 보다는 1로 향하도록 했습니다.(two-sided penalty). 1이라는 특정값으로 제약을 걸어도 실증적으로 봤을 때 이러한 penalty가 critic을 많이 규제하지 않는 것처럼 보인다고 합니다. 그 이유로는 최적의 WGAN critic은 $\mathbb{P}_{r}$, $\mathbb{P}_{g}$ 하의 거의 모든 곳에서 gradient norm 1을 가지고 있기 때문일 것이라고 보았습니다. two-sided penalty는 optimal critic이기 위한 one-sided penalty보다 더 엄격한 조건입니다. one-sided penalty는 critic이 1-Lipschitz function이도록 하는 것이고 two-sided penalty는 optimal critic이도록 하는 것 입니다. 본래 proposition 1에서 보인 것처럼 특정영역에서 gradent의 크기는 거의 대부분 1이기 때문에 gradient penalty를 1이 되도록 주었지만 WGAN에서 이야기한 것은 critic이 1-Lipschitz function이라는 것 뿐입니다. critic이 1-Lipschitz function이기 위해서는 one-sided penalty면 충분하지만 WGAN-GP에서는 optimal critic의 특징을 탐구하여 더 엄격한 two-sided penalty를 주어 딱 1이 되도록 한 것이고 논문에서는 이렇게 엄격한 조건을 주더라도 지나친 규제를 하는게 아니라는 이야기를 하는 것 입니다.

Untitled

Experiments

Training random architectures within a set

DCGAN의 기본 구조에서 약간의 수정을 하여 아래와 같이 모델을 구성하였습니다.

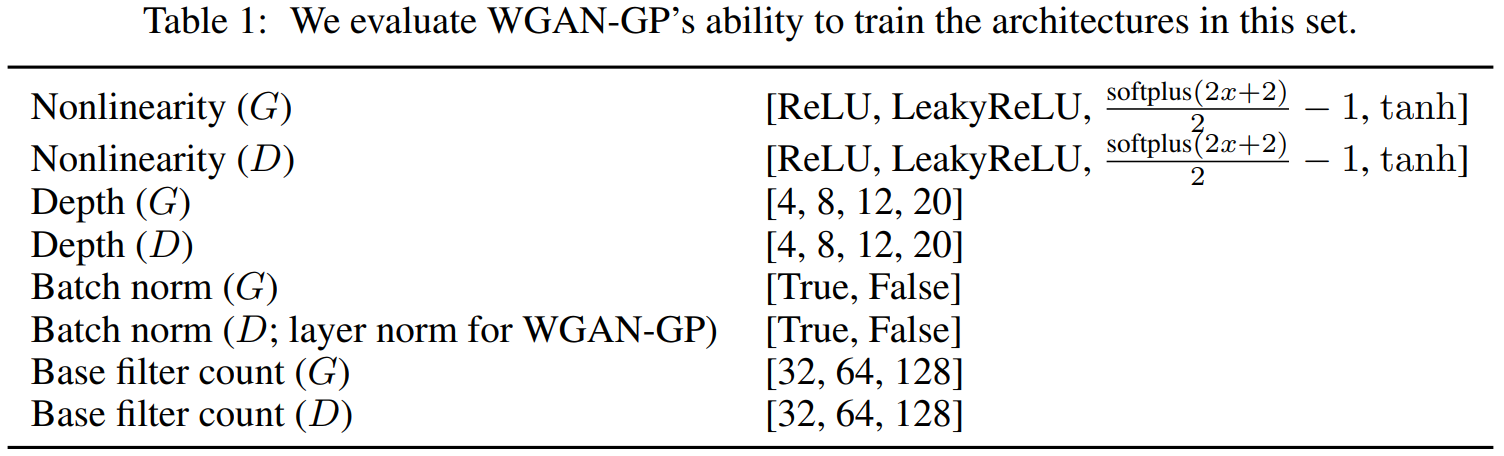
Untitled

이러한 구성에서 32*32 ImageNet으로 학습시켰고 WGAN-GP, standard GAN objectives를 사용하여 학습시켰습니다. 그리고 min_score를 정하고 생성한 이미지의 inception_score가 min_score를 넘으면 성공으로 판단하여 실험을 진행하였습니다. inception_score는 높을 수록 좋습니다.

논문에서 제안한 핵심주장은 loss에 Gradient penalty term을 추가하는 것입니다. 때문에 특정 architectures에서 만이 아니라 다양한 구성의 architectures에서도 좋다는 것을 보이기 위해 이러한 비교방식을 채택했습니다.

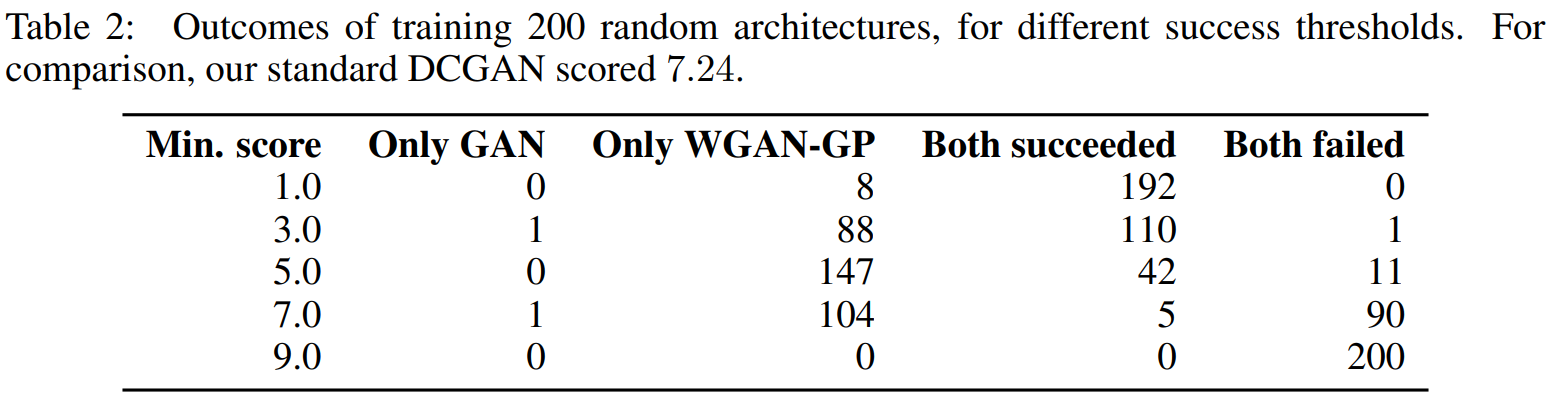
Untitled

WGAN-GP의 성능이 더 좋은 것을 확인할 수 있습니다.

Training varied architectures on LSUN bedrooms

Untitled

WGAN-GP loss를 사용하면 학습이 잘 되는 것을 볼 수 있습니다.

Improved performance over weight clipping

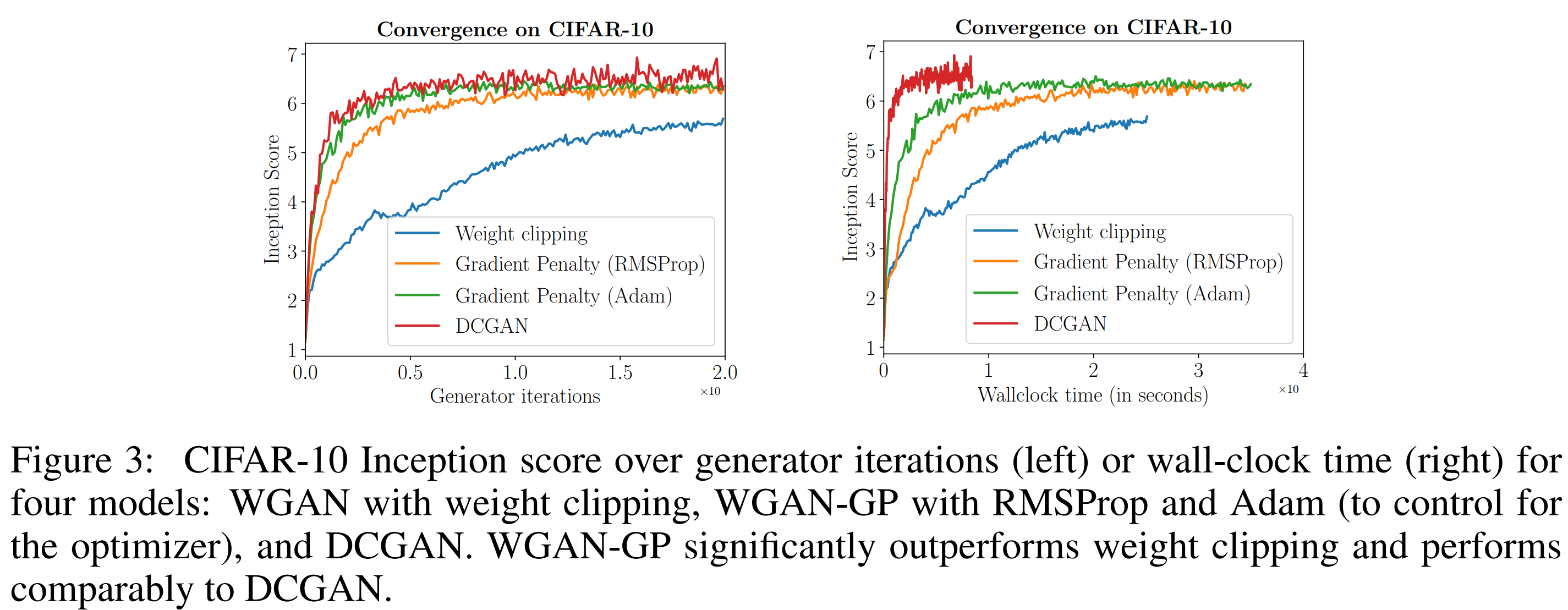
Untitled

왼쪽은 iteration에 따른 Inception Score이고 오른쪽은 시간에 따른 Inception Score입니다. WGAN-GP는 weight clipping보다 성능이 좋은 것을 볼 수 있습니다.

Modeling discrete data with a continuous generator

모델의 degenerate distributions을 모델링 할 수 있는 능력을 보이기 위하여 샘플링을 사용하지 않고 복잡한 이산 확률 분포를 모델링 하도록 훈련 시킵니다. Google Billion Word dataset을 사용하고 1D CNN와 softmax를 모델에 적용하였습니다.

Untitled

모델은 별도의 샘플링 없이 latent vector로 부터 직접 one-hot character embedding하는 것을 학습한다. 기존의 GAN과는 비교할 만한 결과를 얻지는 못했습니다.

보통 확률 분포의 모수를 추정하고 여기서 샘플링하는 방식을 사용하지만 WGAN-GP의 경우 모델이 곧바로 각 문자의 확률을 반환합니다. 이렇게 하더라도 학습이 가능하다는 것입니다.

loss

critic loss는 $\underbrace{\mathbb{E}{\tilde x \sim \mathbb{P}_g}[D(\tilde x)]-\mathbb{E}{x \sim \mathbb{P}r}[D(x)]}{\text{WGAN의 critic loss}}$입니다. Negative Critic loss는 critic의 성능이 좋을 수록 증가합니다. WGAN loss에서 잘 들어나는 특징인데 WGAN-GP에서도 이 특징이 유지됩니다. 이러한 점을 보이기 위해 적은 데이터로 overfitting시키는 실험을 진행하였습니다. 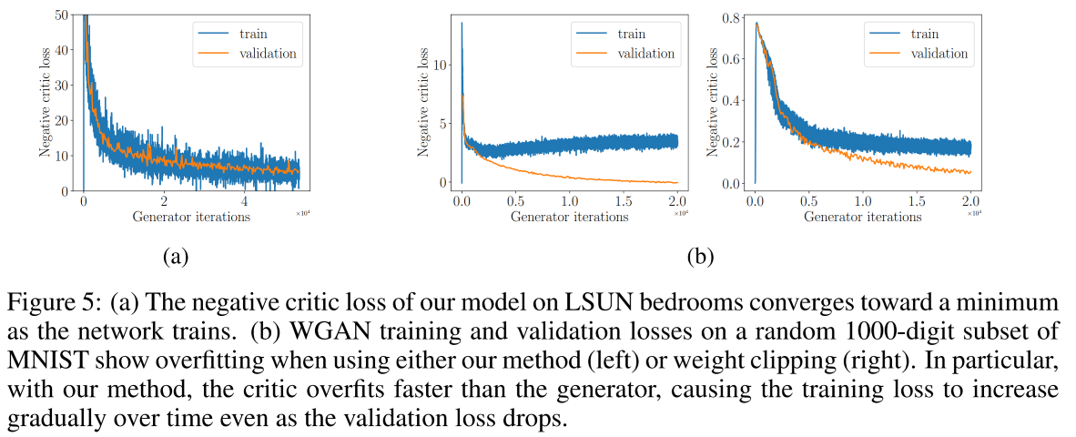그림1 우측 b가 overfitting시킨 WGAN-GP(좌측), WGAN(우측)입니다. 적은 real data에 overfitting되면서 증가하는 모습을 보이지만 validation용 real data와 generated data를 입력받게 되면 성능이 떨어졌음을 알 수 있습니다. 이를 통해 critic이 overfitting되는 상황에서도 generator의 학습이 가능하며 WGAN-GP의 경우 더 잘 학습하기 때문에 WGAN과 달리 overfitting하면서 negative critic loss가 증가하는 것을 확인할 수 있었습니다.

Conclusion

WGAN은 discriminator와 generator가 학습과정에서 균형을 이루지 않아도 학습이 가능하게 했습니다. WGAN에서는 1-립시츠조건을 만족하기 위해 weight clipping을 사용했습니다. WGAN-GP에서는 weight clipping의 문제를 확인하고 동일한 문제를 나타내지 않는 Gradient penalty를 통한 개선안을 제안하였습니다. 이를 통해 GAN을 안정적으로 학습시킬 수 있는 방안을 마련하였습니다. 이러한 GAN을 훈련하기 위한 보다 안정적인 알고리즘을 이용하여 대규모 이미지 데이터 세트를 이용한 더 복잡한 모델의 가능성을 열었다는 의미가 있다고 할 수 있습니다.

장단점

장점:

WGAN의 문제를 잘 해결하였습니다. WGAN-GP의 파급력은 굉장히 큽니다. StyleGAN과 PGGAN과 같은 규모가 크고 복잡한 GAN을 학습시키는데 사용되었습니다. GAN을 학습시키고자 할때 WGAN-GP를 사용하면 상당히 안정적으로 학습하는 것을 확인할 수 있습니다.

단점:

discrete data with a continuous generator의 결과는 다소 의문이 듭니다. 다른 text generator와의 비교나 WGAN-GP를 사용하지 않을 때 학습이 이뤄지지 않은 것을 보여 주었으면 좋았을 것 같습니다.

의미

WGAN-GP loss는 학습을 상당히 안정적으로 만들어 주기 때문에 PGGAN부터 시작하여 대부분의 GAN모델에서 자주 사용되는 loss함수가 되었습니다.

Untitled

PGGAN은 WGAN-GP를 사용하여 안정적으로 1024*1024 해상도의 이미지를 생성할 수 있었습니다.

활용

WGAN-GP는 이미지 합성 외에 음성 합성, 추천 시스템에도 활용되었습니다.

음성 합성: 다화자 음성합성

Wasserstein GAN and Waveform Loss-based Acoustic Model Training for Multi-speaker Text-to-Speech Synthesis Systems Using a WaveNet Vocoder